SSBU Icon.png

Greninja (SSBU): Difference between revisions

From SmashWiki, the Super Smash Bros. wiki
Jump to navigationJump to search
(Undid edit by Cookies and Creme: u also gonna fite me)
Tag: Undo
m (Reverted edits by Thequantumharmonicoscillator (talk) to last version by Cookies and Creme.)
Tag: Rollback
Line 1: Line 1:
{{Use American English|date = February 2019}}
{{ArticleIcons|ultimate=y}}
{{Short description|Important, well-understood quantum mechanical model}}
{{disambig2|Greninja's appearance in ''Super Smash Bros. Ultimate''|the character in other contexts|Greninja}}
{{Quantum mechanics}}
{{Infobox Character
{{redirect|QHO|text=It is also the [[IATA airport code]] for [[Transportation in Houston#Airports|all airports in the Houston area]]}}
|name = Greninja
 
|image = [[File:Greninja SSBU.png|250px]]
[[File:QuantumHarmonicOscillatorAnimation.gif|thumb|300px|right|Some trajectories of a [[harmonic oscillator]] according to [[Newton's laws]] of [[classical mechanics]] (A–B), and according to the [[Schrödinger equation]] of [[quantum mechanics]] (C–H). In A–B, the particle (represented as a ball attached to a [[Hooke's law|spring]]) oscillates back and forth. In C–H, some solutions to the Schrödinger Equation are shown, where the horizontal axis is position, and the vertical axis is the real part (blue) or imaginary part (red) of the [[wavefunction]]. C, D, E, F, but not G, H, are [[energy eigenstate]]s. H is a [[Coherent states|coherent state]]—a quantum state that approximates the classical trajectory.]]
|game = SSBU
 
|ssbgame1 = SSB4
The '''quantum harmonic oscillator''' is the [[quantum mechanics|quantum-mechanical]] analog of the [[harmonic oscillator|classical harmonic oscillator]]. Because an arbitrary smooth [[Potential energy|potential]] can usually be approximated as a [[Harmonic oscillator#Simple harmonic oscillator|harmonic potential]] at the vicinity of a stable [[equilibrium point]],  it is one of the most important model systems in quantum mechanics. Furthermore, it is one of the few quantum-mechanical systems for which an exact, [[List_of_quantum-mechanical_systems_with_analytical_solutions|analytical solution]] is known.<ref>{{Cite book | author=Griffiths, David J. | title=Introduction to Quantum Mechanics | edition=2nd | publisher=Prentice Hall | year=2004 | isbn=978-0-13-805326-0 | author-link=David Griffiths (physicist) | url-access=registration | url=https://archive.org/details/introductiontoel00grif_0 }}</ref><ref>{{Cite book| author=Liboff, Richard L. | title=Introductory Quantum Mechanics | publisher=Addison–Wesley | year=2002 | isbn=978-0-8053-8714-8| author-link=Liboff, Richard L.}}</ref><ref>{{Cite web | last =Rashid | first =Muneer A. | author-link =Munir Ahmad Rashid | title =Transition amplitude for time-dependent linear harmonic oscillator with Linear time-dependent terms added to the Hamiltonian | website =M.A. Rashid – [[National University of Sciences and Technology, Pakistan|Center for Advanced Mathematics and Physics]] | publisher =[[National Center for Physics]] | year =2006 | url =http://www.ncp.edu.pk/docs/12th_rgdocs/Munir-Rasheed.pdf | format =[[PDF]]-[[Microsoft PowerPoint]] | access-date =19 October 2010 }}</ref>
|availability = [[Unlockable character|Unlockable]]
 
}}
==One-dimensional harmonic oscillator==
'''Greninja''' ({{ja|ゲッコウガ|Gekkōga}}, ''Gekkouga'') is a playable character in ''[[Super Smash Bros. Ultimate]]''. It was officially revealed on June 12th, 2018 alongside {{SSBU|Mr. Game & Watch}} and the rest of the returning roster. Greninja is classified as [[Fighter number|Fighter #50]].
 
===Hamiltonian and energy eigenstates===
[[Image:HarmOsziFunktionen.png|thumb|Wavefunction representations for the first eight bound eigenstates, ''n'' = 0 to 7. The horizontal axis shows the position ''x''.]]
[[Image:Aufenthaltswahrscheinlichkeit harmonischer Oszillator.png|thumb|Corresponding probability densities.]]
 
The [[Hamiltonian (quantum mechanics)|Hamiltonian]] of the particle is:
<math display="block">\hat H = \frac{{\hat p}^2}{2m} + \frac{1}{2} k {\hat x}^2 = \frac{{\hat p}^2}{2m} + \frac{1}{2} m \omega^2 {\hat x}^2 \, ,</math>
where {{mvar|m}} is the particle's mass, {{mvar|k}} is the force constant, <math display="inline">\omega = \sqrt{k / m}</math> is the [[angular frequency]] of the oscillator, <math>\hat{x}</math> is the [[position operator]] (given by {{mvar|x}} in the coordinate basis), and <math>\hat{p}</math>  is the [[momentum operator]] (given by <math>\hat p = -i \hbar \, \partial / \partial x</math> in the coordinate basis). The first term in the Hamiltonian represents the kinetic energy of the particle, and the second term represents its potential energy, as in [[Hooke's law]].
 
One may write the time-independent [[Schrödinger equation]],
<math display="block"> \hat H \left| \psi \right\rangle = E \left| \psi \right\rangle  ~,</math>
where {{mvar|E}} denotes a to-be-determined real number that will specify a time-independent [[energy level]], or [[eigenvalue]], and the solution  {{math|{{!}}''ψ''⟩}} denotes that level's energy [[eigenstate]].
 
One may solve the differential equation representing this eigenvalue problem in the coordinate basis, for the [[wave function]] {{math|1=⟨''x''{{!}}''ψ''⟩ = ''ψ''(''x'')}}, using a [[spectral method]]. It turns out that there is a family of solutions. In this basis, they amount to [[Hermite polynomials#Hermite functions| Hermite functions]],
<math display="block"> \psi_n(x) = \frac{1}{\sqrt{2^n\,n!}}  \left(\frac{m\omega}{\pi \hbar}\right)^{1/4}  e^{
- \frac{m\omega x^2}{2 \hbar}} H_n\left(\sqrt{\frac{m\omega}{\hbar}} x \right), \qquad n = 0,1,2,\ldots. </math>
 
The functions ''H<sub>n</sub>'' are the physicists' [[Hermite polynomials]],
<math display="block">H_n(z)=(-1)^n~ e^{z^2}\frac{d^n}{dz^n}\left(e^{-z^2}\right).</math>
 
The corresponding energy levels are
<math display="block"> E_n = \hbar \omega\bigl(n + \tfrac{1}{2}\bigr)=(2 n + 1) {\hbar \over 2} \omega~.</math>
 
This energy spectrum is noteworthy for three reasons.  First, the energies are quantized, meaning that only discrete energy values (integer-plus-half multiples of {{math|''ħω''}}) are possible; this is a general feature of quantum-mechanical systems when a particle is confined. Second, these discrete energy levels are equally spaced, unlike in the [[Bohr model]] of the atom, or the [[particle in a box]]. Third, the lowest achievable energy (the energy of the {{math|1=''n'' = 0}} state, called the [[ground state]]) is not equal to the minimum of the potential well, but {{math|''ħω''/2}} above it; this is called [[zero-point energy]]. Because of the zero-point energy, the position and momentum of the oscillator in the ground state are not fixed (as they would be in a classical oscillator), but have a small range of variance, in accordance with the [[Heisenberg uncertainty principle]].
 
The ground state probability density is concentrated at the origin, which means the particle spends most of its time at the bottom of the potential well, as one would expect for a state with little energy. As the energy increases, the probability density peaks at the classical "turning points", where the state's energy coincides with the potential energy. (See the discussion below of the highly excited states.) This is consistent with the classical harmonic oscillator, in which the particle spends more of its time (and is therefore more likely to be found) near the turning points, where it is moving the slowest. The [[correspondence principle]] is thus satisfied. Moreover, special nondispersive [[wave packet]]s, with minimum uncertainty,  called [[Coherent states#The wavefunction of a coherent state|coherent states]] oscillate very much like classical objects, as illustrated in the figure; they are ''not'' eigenstates of the Hamiltonian.
 
===Ladder operator method===
[[Image:QHarmonicOscillator.png|right|thumb|Probability densities <nowiki>|</nowiki>''ψ<sub>n</sub>''(''x'')<nowiki>|</nowiki><sup>2</sup> <!--or in pseudoTeX: <math>\left |\psi_n(x)\right |^2</math> --> for the bound eigenstates, beginning with the ground state (''n'' = 0) at the bottom and increasing in energy toward the top. The horizontal axis shows the position {{mvar|x}}, and brighter colors represent higher probability densities.]]
 
The "[[ladder operator]]" method, developed by [[Paul Dirac]], allows extraction of the energy eigenvalues without directly solving the differential equation. It is generalizable to more complicated problems, notably in [[quantum field theory]].  Following this approach, we define the operators {{mvar|a}} and its [[Hermitian adjoint|adjoint]] {{math|''a''<sup>†</sup>}},
<math display="block">\begin{align}
          a &=\sqrt{m\omega \over 2\hbar} \left(\hat x + {i \over m \omega} \hat p \right) \\
  a^\dagger &=\sqrt{m\omega \over 2\hbar} \left(\hat x - {i \over m \omega} \hat p \right)
\end{align}</math>Note these operators classically are exactly the [[Generator (mathematics)|generators]] of normalized rotation in the phase space of <math>x</math> and <math>m\frac{dx}{dt}</math>, ''i.e'' they describe the forwards and backwards evolution in time of a classical harmonic oscillator.
 
These operators lead to the useful representation of <math>\hat{x}</math> and  <math>\hat{p}</math>,
<math display="block">\begin{align}
  \hat x &=  \sqrt{\frac{\hbar}{2 m\omega}}(a^\dagger + a) \\
  \hat p &= i\sqrt{\frac{\hbar m \omega}{2}}(a^\dagger - a) ~.
\end{align}</math>
 
The operator {{mvar|a}} is not [[Hermitian operator|Hermitian]], since itself and its adjoint {{math|''a''<sup>†</sup>}} are not equal. The energy eigenstates {{math|{{ket|''n''}}}} (also known as [[Fock state|Fock states]]), when operated on by these ladder operators, give
<math display="block">\begin{align}
  a^\dagger|n\rangle &= \sqrt{n + 1} | n + 1\rangle \\
          a|n\rangle &= \sqrt{n} | n - 1\rangle.
\end{align}</math>


It is then evident that {{math|''a''<sup>†</sup>}}, in essence, appends a single quantum of energy to the oscillator, while {{mvar|a}} removes a quantum. For this reason, they are sometimes referred to as "creation" and "annihilation" operators.
Billy Bob Thompson, Yūji Ueda, Frédéric Clou and Benedikt Gutjan's portrayals of Greninja from ''Super Smash Bros. 4'' were repurposed for the English, Japanese, French and German versions of ''Ultimate'', respectively.


From the relations above, we can also define a number operator {{mvar|N}}, which has the following property:
==How to unlock==
<math display="block">\begin{align}
Complete one of the following:
                        N &= a^\dagger a \\
*Play [[VS. match]]es, with Greninja being the 58th character to be unlocked.
  N\left| n \right\rangle &= n\left| n \right\rangle.
*Clear {{SSBU|Classic Mode}} with {{SSBU|Donkey Kong}} or any character in his unlock tree, being the 6th character unlocked after {{SSBU|Sheik}}.
\end{align}</math>
*Have Greninja join the player's party in [[World of Light]].
Greninja must then be defeated on [[Kalos Pokémon League]] (the [[Ω form]] is used in World of Light).


The following [[commutator]]s can be easily obtained by substituting the [[canonical commutation relation]],
==Attributes==
<math display="block">[a, a^\dagger] = 1,\qquad[N, a^\dagger] = a^{\dagger},\qquad[N, a] = -a, </math>
Greninja, true to being a ninja-themed character, has very strong mobility; it has the 8th fastest [[dash|run speed]], the 10th fastest [[air speed]], is tied for the 9th fastest [[fall speed|falling ]] (and [[fast fall|fast falling]]) speed, the 2nd highest [[gravity]], and possesses the 2nd highest [[jump|jump height]] overall. However, unlike most characters who boast similar mobility (such as {{SSBU|Sheik}}), Greninja boasts a surprising amount of KO options, good range on plenty of its attacks, and KO throws.


And the Hamilton operator can be expressed as
One of Greninja's most notable traits is its high mobility which complements its grounded moveset. Greninja's dash attack comes out on frame 7 and has very low ending lag, as well as the ability to cross upon shields. Its knockback angle allows for many true follow-ups and strings over a large range of percents. Its neutral jab attack comes out on frame 3, making it a good grounded combo breaker. It can also lock, which gives Greninja access to potent punishes from opponents missing techs. Its down tilt is an excellent combo starter due to its low startup, ending lag and vertical launch angle. Greninja's up tilt is a frame 9 disjointed hitbox that acts well as an anti-air and can also be a combo starter. Its smash attacks are also reliable in their own right; its forward smash is quick for its range and power, down smash is an excellent punishment option for ledge regrabs, as well as sending at a low angle, and up smash is a potent combo finisher.
<math display="block">\hat H = \hbar\omega\left(N + \frac{1}{2}\right),</math>


so the eigenstate of {{mvar|N}} is also the eigenstate of energy.
Greninja also has a very strong air game due to its aforementioned air speed and jump height. Greninja's aerials are reliable for multiple situations and all have low landing lag (except for down aerial, at 30 frames). Its neutral aerial is a decent low percent combo starter due to it having incredibly low landing lag and a good launch angle. It can also KO at high percentages. Its forward aerial acts as a combo finisher from its combo starters and can KO moderately early. Forward aerial's low landing lag and disjointed nature also make it safe on shield in many situations when spaced correctly. Its up aerial is a great juggling option with low all-around lag and boasting good KO potential near the upper blast line. Greninja can also utilize its multihits to drag down opponents to create tech chase and jab lock situations. Its back aerial is a very fast follow up or offstage edgeguarding option. Down aerial can be used as a mix up to return to the stage from far above, as well as perform surprise combos on hit with both its [[meteor smash]] and sourspot hitbox.


The commutation property yields
Greninja's grab game is overall very effective, due to its grabs being among the longest ranges of any non-tether grab in the game. Its forward, up, and back throws can KO at high percentages. Down throw acts as a middle percent combo starter, as well as a strong DI mix up, especially at higher percentages at ledge as a 50/50 between DI in and out in conjunction with forward throw. Up throw acts as a versatile combo starter that can lead to juggling situations. Because of this, Greninja has plenty of options off of a grab, as not one of its throws could be considered useless.
<math display="block">\begin{align}
  Na^{\dagger}|n\rangle &= \left(a^\dagger N + [N, a^\dagger]\right)|n\rangle \\
                        &= \left(a^\dagger N + a^\dagger\right)|n\rangle \\
                        &= (n + 1)a^\dagger|n\rangle,
\end{align} </math>


and similarly,
Finally, Greninja's special moves are effective in various situations. [[Water Shuriken]] acts as a versatile zoning tool, as well as a high-percentage KO option when fully charged. At low-to-mid percents, it is also a combo starter, allowing Greninja to rush down its opponent and follow up with any aerial attack or an up smash. [[Shadow Sneak]] works as an effective recovery mix up, as well as a potent KO move from a good read or pseudo-combo finisher. Despite lacking an offensive hitbox, [[Hydro Pump]] is a good recovery move for its long distance, and can be used for gimping recoveries due to having windbox properties. [[Substitute]] is a counterattack with the unique attribute of being able to be aimed in one of 8 different directions upon a successful counter. These angled follow ups allow for Greninja to gain pseudo-follow ups as well as KO earlier by picking the optimal angle in regards to stage positioning.
<math display="block">Na|n\rangle = (n - 1)a | n \rangle.</math>


This means that {{mvar|a}} acts on  {{math|{{!}}''n''⟩}}  to produce, up to a multiplicative constant,  {{math|{{!}}''n''–1⟩}}, and {{math|''a''<sup>†</sup>}} acts on  {{math|{{!}}''n''⟩}} to produce {{math|{{!}}''n''+1⟩}}. For this reason, {{mvar|a}} is called a '''annihilation operator''' ("lowering operator"), and {{math|''a''<sup>†</sup>}} a '''creation operator''' ("raising operator"). The two operators together are called [[ladder operator]]s. In quantum field theory, {{mvar|a}} and {{math|''a''<sup>†</sup>}} are alternatively called "annihilation" and "creation" operators because they destroy and create particles, which correspond to our quanta of energy.
Like all characters, Greninja is flawed in many ways. One of Greninja's primary flaws is its inability to break out of disadvantage state. While not as bad as the previous game, Greninja still has difficulties escaping combos due to its fast falling speed and its aerials still having relatively high startup. This can sometimes be alleviated with its back or down aerials, but both are not very effective due to back aerial's almost entirely horizontal hitboxes and down aerial's landing lag. Another option is aerial Water Shuriken, which stalls Greninja in the air and can be used as a landing mix up, as well as Hydro Pump landing mix ups.  


Given any energy eigenstate, we can act on it with the lowering operator, {{mvar|a}}, to produce another eigenstate with {{math|''ħω''}} less energy. By repeated application of the lowering operator, it seems that we can produce energy eigenstates down to {{math|1=''E'' = −∞}}. However, since
Greninja's biggest weakness however, is its terrible out of shield game, which is arguably the worst of the entire cast. Because of its high short hop, its aerials slow startup, and lacking a fast grab (although it has good range), Greninja lacks an effective out of shield option faster than frame 14. While its back aerial is fairly quick at frame 5 (making it frame 8 out of shield), it is unable to hit opponents in front of Greninja and is very inconsistent at hitting opponents behind Greninja due to its high short hop. Jumping or rolling out of shield are potential options to reset neutral, but they are very predictable and easily read. Thus, when Greninja is pinned down in shield, it has difficulty escaping the situation without being heavily punished. Combined with its vulnerability to combos, this gives it an atrocious defensive game.
<math display="block">n = \langle n | N | n \rangle = \langle n | a^\dagger a | n \rangle = \Bigl(a | n \rangle \Bigr)^\dagger a | n \rangle \geqslant 0,</math>


the smallest eigen-number is 0, and
Altogether, Greninja's playstyle requires players to think like an actual ninja: utilizing Greninja's superb mobility and fast attacks to rush down opponents, saving the slower attacks for potential mixups, mindgames and surprise KO options, and remaining unpredictable to prevent being trapped into disadvantageous positions.
<math display="block">a \left| 0 \right\rangle = 0. </math>


In this case, subsequent applications of the lowering operator will just produce zero kets, instead of additional energy eigenstates. Furthermore, we have shown above that
==Changes from ''[[Super Smash Bros. 4]]''==
<math display="block">\hat H \left|0\right\rangle = \frac{\hbar\omega}{2} \left|0\right\rangle</math>
Greninja has been greatly buffed from ''Smash 4'' to ''Ultimate''. Its playstyle's traits have been further improved in the transition, while the general engine changes benefit said playstyle.


Finally, by acting on |0⟩ with the raising operator and multiplying by suitable [[Wave function#Normalization condition|normalization factors]], we can produce an infinite set of energy eigenstates
Most of the universal changes notably benefit Greninja. As with all other characters in the game, Greninja's already quick mobility is faster like most characters, which benefits its hit-and-run playstyle, allowing Greninja to close in the distance and escape to reset the neutral game much more easily. The ability to run cancel into any ground move allows Greninja to further exploit its amazing ground mobility, allowing for easier setups into its combo starters, such as up and down tilt and dash attack. Furthermore, the reduced landing lag on Greninja's aerial attacks gives it an easier time landing, while the universal 3-frame jumpsquat improves Greninja's ground-to-air potential. The implementation of [[spot dodge]] canceling improves its potential punish game, due to its wide variety of combo starters and fast frame data. Finally, the changes to air dodge mechanics slightly improve its previously below average edgeguarding game.
<math display="block">\left\{\left| 0 \right\rangle, \left| 1 \right\rangle, \left| 2 \right\rangle, \ldots , \left| n \right\rangle, \ldots\right\},</math>


such that
Aside from the universal changes, Greninja has also received notable direct buffs. The biggest ones were to its grab game: its standing grab is faster and its pummel, previously one of the worst in ''Smash 4'', deals less damage but is significantly faster, which allows Greninja to deal much more damage before throwing the opponent. Greninja's forward throw has higher knockback, allowing it to KO in an emergency, as with up throw. Its up and down throws also have better combo and juggling potential due to the universal changes to mobility - down throw notably now allows for potential KO confirms into forward and back aerial. Other buffs include [[Water Shuriken]] having more range, improving Greninja's camping ability. Greninja now has a new down tilt that has lower ending lag and sends at more favorable angles, and its dash attack sends at a higher angle, further improving Greninja's combo game. Greninja's KO power has also been buffed, with forward smash and forward aerial receiving higher knockback, up smash connecting better into its second hit, and down smash having faster startup. Lastly, [[Substitute]] now slows opponents down and offers Greninja intangibility during all of its attack variations, bringing it in line with other counterattacks.
<math display="block">\hat H \left| n \right\rangle = \hbar\omega \left( n + \frac{1}{2} \right) \left| n \right\rangle, </math>
which matches the energy spectrum given in the preceding section.


Arbitrary eigenstates can be expressed in terms of |0⟩,
On the other hand, Greninja is not without its nerfs. Notably, the ability to tech footstools has made footstool combos harder to pull off, which hinders Greninja's combo ability (specifically from its down aerial); however, this nerf is alleviated by Greninja's buffed combo game, due to other universal changes that impact it more positively. Substitute's attack variants are all weaker while also being more laggy overall, which compensates for the attack's new intangibility. In exchange for its buffed mobility, Greninja is now lighter, which brings it slightly more in-line with other combo-centric and/or hit-and-run characters, while not compensating much for its vulnerability to combos.
<math display="block">|n\rangle = \frac{(a^\dagger)^n}{\sqrt{n!}} |0\rangle. </math>
{{math proof|<math display="block">\begin{align}
  \langle n | aa^\dagger | n \rangle &= \langle n|\left([a, a^\dagger] + a^\dagger a\right)| n \rangle = \langle n|(N + 1)|n\rangle = n + 1 \\
    \Rightarrow a^\dagger | n\rangle &= \sqrt{n + 1} | n + 1\rangle \\
                    \Rightarrow|n\rangle &= \frac{a^\dagger}{\sqrt{n}} | n - 1 \rangle = \frac{(a^\dagger)^2}{\sqrt{n(n - 1)}} | n - 2 \rangle = \cdots = \frac{(a^\dagger)^n}{\sqrt{n!}}|0\rangle.
\end{align}</math>}}


====Analytical questions====
As a result of receiving multiple buffs with relatively few nerfs, Greninja has improved significantly from ''Smash 4'', and has retained its status as a viable character in ''Ultimate'', with above average representation and some strong results in competitive play thanks to smashers such as {{Sm|iStudying}}, {{Sm|Jw}}, {{Sm|Lea}}, {{Sm|Somé}}, and {{Sm|Stroder}}. Because of this, Greninja is considered as a high or even top-tier character by many professional players.


The preceding analysis is algebraic, using only the commutation relations between the raising and lowering operators. Once the algebraic analysis is complete, one should turn to analytical questions. First, one should find the ground state, that is, the solution of the equation <math>a\psi_0 = 0</math>. In the position representation, this is the first-order differential equation
{{SSB4 to SSBU changelist|char=Greninja}}
<math display="block">\left(x+\frac{\hbar}{m\omega}\frac{d}{dx}\right)\psi_0 = 0,</math>
whose solution is easily found to be the Gaussian<ref>The normalization constant is <math>C = \left(\frac{m\omega}{\pi \hbar}\right)^{\frac{1}{4}}</math>, and satisfies the normalization condition <math>\int_{-\infty}^{\infty}\psi_0(x)^{*}\psi_0(x)dx = 1</math>.</ref>
<math display="block">\psi_0(x)=Ce^{-\frac{m\omega x^2}{2\hbar}}.</math>
Conceptually, it is important that there is only one solution of this equation; if there were, say, two linearly independent ground states, we would get two independent chains of eigenvectors for the harmonic oscillator. Once the ground state is computed, one can show inductively that the excited states are Hermite polynomials times the Gaussian ground state, using the explicit form of the raising operator in the position representation. One can also prove that, as expected from the uniqueness of the ground state, the Hermite functions energy eigenstates <math>\psi_n</math> constructed by the ladder method form a ''complete'' orthonormal set of functions.<ref>See Theorem 11.4 in {{citation|first=Brian C.|last=Hall|title=Quantum Theory for Mathematicians|series=Graduate Texts in Mathematics|volume=267|isbn=978-1461471158 |publisher=Springer|year=2013}}</ref>


Explicitly connecting with the previous section, the ground state  |0⟩  in the position representation is determined by <math> a| 0\rangle =0</math>,
==Update history==
<math display="block">  \left\langle x \mid a \mid 0 \right\rangle = 0 \qquad
Greninja has received a mix of minor buffs and nerfs via game updates. Several glitches have also been fixed over time.
  \Rightarrow \left(x + \frac{\hbar}{m\omega}\frac{d}{dx}\right)\left\langle x\mid 0\right\rangle = 0 \qquad
  \Rightarrow          </math>
<math display="block"> \left\langle x\mid 0\right\rangle = \left(\frac{m\omega}{\pi\hbar}\right)^\frac{1}{4} \exp\left( -\frac{m\omega}{2\hbar}x^2 \right)
    = \psi_0  ~,</math>
hence
<math display="block"> \langle x \mid a^\dagger \mid 0 \rangle = \psi_1 (x) ~,</math>
so that <math>\psi_1(x,t)=\langle x \mid e^{-3i\omega t/2} a^\dagger \mid 0 \rangle </math>, and so on.


===Natural length and energy scales===
'''{{GameIcon|ssbu}} {{SSBU|1.2.0}}'''
The quantum harmonic oscillator possesses natural scales for length and energy, which can be used to simplify the problem. These can be found by [[nondimensionalization#Quantum harmonic oscillator|nondimensionalization]].
{{UpdateList (SSBU)/1.2.0|char=Greninja}}


The result is that, if  ''energy'' is measured in units of  {{math|''ħω''}} and ''distance'' in units of {{math|{{sqrt|''ħ''/(''mω'')}}}}, then the Hamiltonian simplifies to
'''{{GameIcon|ssbu}} {{SSBU|2.0.0}}'''
<math display="block"> H = -\frac{1}{2} {d^2 \over dx^2} +\frac{1}{2}  x^2 ,</math>
{{UpdateList (SSBU)/2.0.0|char=Greninja}}
while the energy eigenfunctions and eigenvalues simplify to Hermite functions and integers offset by a half,
<math display="block">\psi_n(x)= \left\langle x \mid n \right\rangle = {1 \over \sqrt{2^n n!}}~ \pi^{-1/4} \exp(-x^2 / 2)~ H_n(x),</math>
<math display="block">E_n = n + \tfrac{1}{2} ~,</math>
where {{math|''H''<sub>''n''</sub>(''x'')}} are the [[Hermite polynomials]].


To avoid confusion,  these "natural units"  will mostly not be adopted in this article. However, they frequently come in handy when performing calculations, by bypassing clutter.
'''{{GameIcon|ssbu}} {{SSBU|3.0.0}}'''
{{UpdateList (SSBU)/3.0.0|char=Greninja}}


For example, the [[fundamental solution]] ([[Propagator#Basic_examples:_propagator_of_free_particle_and_harmonic_oscillator|propagator]]) of {{math|''H'' − ''i∂<sub>t</sub>''}}, the time-dependent Schrödinger operator for this oscillator, simply boils down to the [[Mehler kernel]],<ref>[[Wolfgang Pauli|Pauli, W.]]  (2000), ''Wave Mechanics: Volume 5 of Pauli Lectures on Physics'' (Dover Books on Physics). {{ISBN|978-0486414621}} ; Section 44.</ref><ref>[[Edward Condon|Condon, E. U.]]  (1937). "Immersion of the Fourier transform in a continuous group of functional transformations", ''Proc. Natl. Acad. Sci. USA''  '''23''', 158–164. [https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1076889/pdf/pnas01779-0028.pdf online]</ref>
'''{{GameIcon|ssbu}} {{SSBU|3.1.0}}'''
<math display="block">\langle x \mid \exp (-itH) \mid y \rangle \equiv K(x,y;t)= \frac{1}{\sqrt{2\pi i \sin t}} \exp \left(\frac{i}{2\sin t}\left ((x^2+y^2)\cos t - 2xy\right )\right )~,</math>
{{UpdateList (SSBU)/3.1.0|char=Greninja}}
where {{math|1= ''K''(''x'',''y'';0) = ''δ''(''x'' − ''y'')}}. The most general solution for a given initial configuration {{math|''ψ''(''x'',0)}} then is simply
<math display="block">\psi(x,t)=\int dy~ K(x,y;t) \psi(y,0) \,.</math>
{{see also|Path integral formulation#Simple harmonic oscillator}}


===Coherent states===
'''{{GameIcon|ssbu}} {{SSBU|4.0.0}}'''
{{UpdateList (SSBU)/4.0.0|char=Greninja}}


{{main|Coherent state}}
'''{{GameIcon|ssbu}} {{SSBU|7.0.0}}'''
{{UpdateList (SSBU)/7.0.0|char=Greninja}}


[[File:QHO-coherentstate3-animation-color.gif|thumb|Time evolution of the probability distribution (and phase, shown as color) of a coherent state with &#124;''α''&#124;=3.]]
'''{{GameIcon|ssbu}} {{SSBU|8.0.0}}'''
{{UpdateList (SSBU)/8.0.0|char=Greninja}}


The [[Coherent states#The wavefunction of a coherent state|coherent states]] (also known as Glauber states) of the harmonic oscillator are special nondispersive [[wave packet]]s, with minimum uncertainty {{math|1=''σ<sub>x</sub>'' ''σ<sub>p</sub>'' = {{frac|''ℏ''|2}}}}, whose [[observable]]s' [[Expectation value (quantum mechanics)|expectation values]] evolve like a classical system. They are eigenvectors of the annihilation operator, ''not'' the Hamiltonian, and form an [[Overcompleteness|overcomplete]] basis which consequentially lacks orthogonality.
==Moveset==
* Greninja can [[Crawling|crawl]], [[wall cling]], and [[wall jump]].
''For a gallery of Greninja's hitboxes, see [[Greninja (SSBU)/Hitboxes|here]].''


The coherent states are indexed by {{math|''α'' ∈ '''C'''}} and expressed in the {{math|{{braket|ket|''n''}}}} basis as
{{MovesetTable
 
|neutralname=&nbsp;
<math display="block">|\alpha\rangle = \sum_{n=0}^\infty |n\rangle \langle n | \alpha \rangle = e^{-\frac{1}{2} |\alpha|^2} \sum_{n=0}^\infty\frac{\alpha^n}{\sqrt{n!}} |n\rangle = e^{-\frac{1}{2} |\alpha|^2} e^{\alpha a^\dagger} e^{-{\alpha^* a}} |0\rangle.</math>
|neutralcount=3
 
|neutralinf=y
Because <math>a \left| 0 \right\rangle = 0 </math> and via the Kermack-McCrae identity, the last form is equivalent to a [[Unitary operator|unitary]] [[displacement operator]] acting on the ground state: <math>|\alpha\rangle=e^{\alpha \hat a^\dagger - \alpha^*\hat a}|0\rangle  = D(\alpha)|0\rangle</math>. The [[position space]] wave functions are
|neutral1dmg=2%
 
|neutral2dmg=2%
<math display="block">\psi_\alpha(x')= \left(\frac{m\omega}{\pi\hbar}\right)^{\frac{1}{4}} e^{\frac{i}{\hbar} \langle\hat{p}\rangle_\alpha x' - \frac{m\omega}{2\hbar}(x' - \langle\hat{x}\rangle_\alpha)^2} .</math>
|neutral3dmg=3%
 
|neutralinfdmg=0.5% (loop), 2% (last)
Since coherent states are not energy eigenstates, their time evolution is not a simple shift in wavefunction phase. The time-evolved states are, however, also coherent states but with phase-shifting parameter {{mvar|α}} instead: <math>\alpha(t) = \alpha(0) e^{-i\omega t}</math>.
|neutraldesc=Two alternating palm thrusts followed by a double palm thrust that emits a small blast of water. If button mashed, it is instead followed by a series of knifehand strikes that emit blade-shaped water blasts that concludes with an outward knifehand strike that emits a wide blast of water. It can also be jab canceled, such as into forward tilt, down tilt and forward smash.
 
|ftiltname=&nbsp;
===Highly excited states===
|ftiltdmg=7.3%
{{multiple image
|ftiltdesc=A hook kick which stops half way. It can be angled and can [[lock]] opponents.
| width = 320
|utiltname=&nbsp;
| direction = vertical
|utiltdmg=4.5%
| image1 = Excited_state_for_quantum_harmonic_oscillator.svg
|utiltdesc=Swings its tongue upwards. A good aerial combo starter and juggling tool due to its low knockback and somewhat disjointed hitbox. It can combo into itself at low percents and is a reliable way to connect into up aerial.
| image2 = QHOn30pdf.svg
|dtiltname=&nbsp;
| footer = Wavefunction (top) and probability density (bottom) for the {{math|1=''n'' = 30}} excited state of the quantum harmonic oscillator. Vertical dashed lines indicate the classical turning points, while the dotted line represents the classical probability density.
|dtiltdmg=4%
|dtiltdesc=Does a downward hand sweep. It sends opponents at an upward angle, making it a versatile combo starter. Notably, it can confirm a KO into an up smash rather easily.
|dashname=&nbsp;
|dashdmg=8%
|dashdesc=Does a sweep kick. Is arguably one of the best dash attacks in the game, as it launches opponents at an excellent angle for combos, making it one of Greninja's best combo starters. Reliably combos into back aerial at virtually any percent, and can set up up aerial strings or drag-down combos with up aerial.
|fsmashname=&nbsp;
|fsmashdmg=14%
|fsmashdesc=An inward slash with a water kunai. Deals good knockback and has good range. However, it has notable ending lag.
|usmashname=&nbsp;
|usmashdmg=5% (hit 1), 14% (hit 2 clean center), 11% (hit 2 clean sides), 10% (hit 2 late)
|usmashdesc=Two reverse gripped inward slashes with water kunai, similar to {{SSBU|Sheik}}'s up smash. Greninja's strongest finisher, especially when hit clean. Can be combo'd into from a down-tilt at specific percentages for a KO.
|dsmashname=&nbsp;
|dsmashdmg=13% (kunai), 11% (arms)
|dsmashdesc=Hits both sides with water kunai. Due to it sending opponents at an [[semi-spike]] angle and coming out on frame 11, it is a quick and effective way to set up an edge-guard situation.
|nairname=&nbsp;
|nairdmg=11% (clean), 6% (late)
|nairdesc=Strikes a ninjutsu pose while emitting an exploding water bubble. Despite noticeable start-up lag for a neutral aerial(frame 12), it boasts great combo potential at low to mid percentages with its strong and weak hits and can KO confirm into up-smash at high percents with the weak hit. It can also KO at very high percents with its strong hit.
|fairname=&nbsp;
|fairdmg=14%
|fairdesc=Slashes with a water kunai. It has some start-up and suffers from high end lag, but it is a great tool in the neutral for spacing due to its disjointed hitbox and can be used for KOing. It is also safe on shield if spaced correctly.
|bairname=&nbsp;
|bairdmg= 3% (hit 1), 2.5% (hit 2), 6% (hit 3)
|bairdesc=Kicks backwards three times. It is Greninja's fastest aerial attack, although it is also one of the weakest aerials of its kind. However, this makes it a useful combo tool in return, as it can be followed up from a down throw, down tilt, as well as a dash attack. It can be a situational out-of-shield option if the opponent crosses-up on its shield.
|uairname=&nbsp;
|uairdmg=1.3% (hits 1-5), 3% (hit 6)
|uairdesc=Does a upward corkscrew kick, similar to both {{SSBU|Sheik}}'s and {{SSBU|Joker}}'s up aerials. One of Greninja's best combo and KO tools, as it can juggle and KO effectively due to its great jumping prowess. It also allows for drag-down combos because it's multi-hit properties, although this requires precise timing to land it at the right time, as its final launching hit comes out too fast to set up drag-down combos otherwise.
|dairname=&nbsp;
|dairdmg=8%
|dairdesc=A diving double foot stomp. It acts as a [[stall-then-fall]] and bounces off opponents. The clean hit [[meteor smash]]es opponents while the late hit sends the opponent upwards, allowing for some situational combos.
|grabname=&nbsp;
|grabdesc=Grabs with a whirlpool. While its standing grab is slow, it is among the longest-reaching grabs in the game.
|pummelname=&nbsp;
|pummeldmg=1%
|pummeldesc=Compresses target with water. Decent speed.
|fthrowname=&nbsp;
|fthrowdmg=3.5% (hit 1), 4.5% (throw)
|fthrowdesc=Shoves the opponent forward. Can KO at high percentages near the edge.
|bthrowname=&nbsp;
|bthrowdmg=9%
|bthrowdesc=Greninja leans forward and flings the opponent backwards. Like forward throw, its decent knockback gives it good edgeguarding potential at high percentages.
|uthrowname=&nbsp;
|uthrowdmg=5%
|uthrowdesc=Tosses the opponent upwards. One of Greninja's most useful throws, as it can combo into a up tilt or up aerial at low and medium percents and can even KO at later percents.
|dthrowname=&nbsp;
|dthrowdmg=5%
|dthrowdesc=Slams the opponent onto the ground. It can combo into a down tilt, forward tilt, and dash attack at low percentages. It can combo into back aerial at medium percents and later into forward aerial as well at higher percentages with good timing.
|floorfname=&nbsp;
|floorfdmg=8%
|floorfdesc=Sweep kicks around itself while getting up.
|floorbname=&nbsp;
|floorbdmg=8%
|floorbdesc=Sweep kicks around itself while getting up.
|floortname=&nbsp;
|floortdmg=8%
|floortdesc=Sweep kicks around itself while getting up.
|edgename=&nbsp;
|edgedmg=9%
|edgedesc=Performs a roundhouse kick while climbing up.
|nsname=Water Shuriken
|nsdmg=3%-10.8% (uncharged), 1.0% (fully charged looping hits), 9% (fully charged final hit)
|nsdesc=Uses Water Shuriken, which can be charged. Depending on how long the move is charged, the shuriken will be larger and do more damage, however the speed and distance will decrease as a result. At full charge, it hits multiple times and can kill with a Shadow Sneak follow-up at low and medium percents. It is also a decent KOing option at higher percents. A fully charged water shuriken that is reflected at a higher speed will have trouble landing the final hit on Greninja because of the looping hits not moving Greninja far enough for it.
|ssname=Shadow Sneak
|ssdmg=10% (normal), 12% (reverse)
|ssdesc=Disappears briefly, then preforms a forward kick or a drop kick (relative to the user's reappearance in relation to the enemy) to attack. The move activates when the special button is released. The way the shadow moves is relative to Greninja's position, and it can be moved further or closer to change how far Greninja teleports. While performing Shadow Sneak, Greninja cannot run, attack, grab, dodge or shield. However, it can walk slowly, jump and taunt. Has strong knockback and base knockback, which allows it to kill notably early when hitting the move offstage.
|usname=Hydro Pump
|usdmg=2% (per shot)
|usdesc=Uses Hydro Pump to propel itself in the inputted direction; it can be used twice. Each shot has a [[windbox]] effect that pushes opponents, making it a decent option for gimping predictable recoveries.
|dsname=Substitute
|dsdmg=14% (up or down), 11% (left or right)
|dsdesc=Does a pose, and if anyone hits it while posing, Greninja will temporarily disappear, get replaced by a wooden log or a Substitute doll, and then appear behind the opponent and strike them. It deviates noticeably from other counters, as the attack itself can be angled in an inputted direction and launching the opponent in that direction (with the down input meteor smashing opponents, which makes it a good punish against reckless edgeguarders).
|fsname=Secret Ninja Attack
|fsdmg=6% (the mat), 50% (Total in the attack after mat)
|fsdesc=Turns into Ash-Greninja and attacks the opponent with a mat. If an opponent is caught in the mat, Greninja will send them up into the air and strike the opponent repeatedly in midair with its kunai, before slamming them down with a final hit.
|game=SSBU
|dtauntname=
|dtauntdmg=0.5%
|dtauntdesc=While standing on one foot, Greninja holds out its hands, faces the screen, and summons small sprays of water. The sprays produce some knockback, though they're able to KO only at above 420%. A video showing the exact KO percentages at which each character can be KO'd can be found [https://www.youtube.com/watch?v=cH7IDQ_8vic here]. Unlike the rest of Greninja's taunts, this one cannot be cancelled (unless Shadow Sneak is being charged before using it).
}}
}}
When {{mvar|n}} is large, the eigenstates are localized into the classical allowed region, that is, the region in which a classical particle with energy {{math|''E''<sub>''n''</sub>}} can move. The eigenstates are peaked near the turning points: the points at the ends of the classically allowed region where the classical particle changes direction. This phenomenon can be verified through [[Hermite_polynomials#Asymptotic_expansion|asymptotics of the Hermite polynomials]],  and also through the [[WKB approximation]].
===[[On-screen appearance]]===
 
*Emerges from a [[Poké Ball]], then performs a ninjutsu hand sign that emits a small burst of water from its hands.
The frequency of oscillation at {{mvar|x}} is proportional to the momentum {{math|''p''(''x'')}} of a classical particle of energy {{math|''E''<sub>''n''</sub>}}  and position {{mvar|x}}.  Furthermore, the square of the amplitude (determining the probability density) is ''inversely'' proportional to  {{math|''p''(''x'')}},  reflecting the length of time the classical particle spends near {{mvar|x}}. The system behavior in a small neighborhood of the turning point does not have a simple classical explanation, but can be modeled using an [[Airy function]]. Using properties of the Airy function,  one may estimate the probability of finding the particle outside the classically allowed region,  to be approximately
<gallery>
<math display="block">\frac{2}{n^{1/3}3^{2/3}\Gamma^2(\tfrac{1}{3})}=\frac{1}{n^{1/3}\cdot  7.46408092658...}</math>
GreninjaOnScreenAppearanceSSBU.gif|Greninja's on-screen appearance
This is also given, asymptotically, by the integral
</gallery>
<math display="block">\frac{1}{2\pi}\int_{0}^{\infty}e^{(2n+1)\left (x-\tfrac{1}{2}\sinh(2x)  \right )}dx ~.</math>
 
===Phase space solutions===
In the [[phase space formulation]] of quantum mechanics, eigenstates of the quantum harmonic oscillator in [[quasiprobability distribution#Fock state|several different representations]] of the [[quasiprobability distribution]] can be written in closed form. The most widely used of these is for the [[Wigner quasiprobability distribution]].
 
The Wigner quasiprobability distribution for the energy eigenstate {{math|{{!}}''n''⟩}} is, in the natural units described above,{{citation needed|date=July 2020}}
<math display="block">F_n(x, p) = \frac{(-1)^n}{\pi \hbar} L_n\left(2(x^2 + p^2)\right) e^{-(x^2 + p^2)} \,,</math>
where ''L<sub>n</sub>'' are the [[Laguerre polynomials]]. This example illustrates how the Hermite and Laguerre polynomials are [[Hermite polynomials#Wigner distributions of Hermite functions|linked]] through the [[Wigner–Weyl transform|Wigner map]].
 
Meanwhile, the [[Husimi_Q_representation|Husimi Q function]] of the harmonic oscillator eigenstates have an even simpler form. If we work in the natural units described above, we have
<math display="block">Q_n(x,p)=\frac{(x^2+p^2)^n}{n!}\frac{e^{-(x^2+p^2)}}{\pi}</math>
This claim can be verified using the [[Segal–Bargmann_space#The Segal.E2.80.93Bargmann transform|Segal–Bargmann transform]]. Specifically, since the [[Segal–Bargmann space#The canonical commutation relations|raising operator in the Segal–Bargmann representation]] is simply multiplication by <math>z=x+ip</math> and the ground state is the constant function 1, the normalized harmonic oscillator states in this representation are simply <math>z^n/\sqrt{n!}</math> . At this point, we can appeal to the formula for the Husimi Q function in terms of the Segal–Bargmann transform.
 
==''N''-dimensional isotropic harmonic oscillator==
The one-dimensional harmonic oscillator is readily generalizable to {{math|''N''}} dimensions, where {{math|1=''N'' = 1, 2, 3, …}}. In one dimension, the position of the particle was specified by a single [[coordinate system|coordinate]], {{math|''x''}}. In {{math|''N''}} dimensions, this is replaced by {{math|''N''}} position coordinates, which we label {{math|''x''<sub>1</sub>, …, ''x''<sub>''N''</sub>}}. Corresponding to each position coordinate is a momentum; we label these {{math|''p''<sub>1</sub>, …, ''p''<sub>''N''</sub>}}. The [[canonical commutation relations]] between these operators are
<math display="block">\begin{align}
{[}x_i , p_j{]} &= i\hbar\delta_{i,j} \\
{[}x_i , x_j{]} &= 0                  \\
{[}p_i , p_j{]} &= 0
\end{align}</math>
 
The Hamiltonian for this system is
<math display="block"> H = \sum_{i=1}^N \left( {p_i^2 \over 2m} + {1\over 2} m \omega^2 x_i^2 \right).</math>
 
As the form of this Hamiltonian makes clear, the {{math|''N''}}-dimensional harmonic oscillator is exactly analogous to {{math|''N''}} independent one-dimensional harmonic oscillators with the same mass and spring constant. In this case, the quantities {{math|''x''<sub>1</sub>, ..., ''x''<sub>''N''</sub>}} would refer to the positions of each of the {{math|''N''}} particles. This is a convenient property of the {{math|''r''<sup>2</sup>}} potential, which allows the potential energy to be separated into terms depending on one coordinate each.
 
This observation makes the solution straightforward. For a particular set of quantum numbers <math>\{n\}\equiv
\{n_1, n_2, \dots, n_N\}</math> the energy eigenfunctions for the {{math|''N''}}-dimensional oscillator are expressed in terms of the 1-dimensional eigenfunctions as:
 
<math display="block">\langle \mathbf{x}|\psi_{\{n\}}\rangle = \prod_{i=1}^N\langle x_i\mid \psi_{n_i}\rangle</math>
 
In the ladder operator method, we define {{math|''N''}} sets of ladder operators,
 
<math display="block">\begin{align}
a_i &= \sqrt{m\omega \over 2\hbar} \left(x_i + {i \over m \omega} p_i \right), \\
a^{\dagger}_i &= \sqrt{m \omega \over 2\hbar} \left( x_i - {i \over m \omega} p_i \right).
\end{align}</math>
 
By an analogous procedure to the one-dimensional case, we can then show that each of the {{math|''a<sub>i</sub>''}} and {{math|''a''<sup>†</sup><sub>''i''</sub>}} operators lower and raise the energy by {{math|''ℏω''}} respectively. The Hamiltonian is
<math display="block">H = \hbar \omega \, \sum_{i=1}^N \left(a_i^\dagger \,a_i + \frac{1}{2}\right).</math>
This Hamiltonian is invariant under the dynamic symmetry group {{math|''U''(''N'')}} (the unitary group in {{math|''N''}} dimensions), defined by
<math display="block">
U\, a_i^\dagger \,U^\dagger = \sum_{j=1}^N  a_j^\dagger\,U_{ji}\quad\text{for all}\quad
U \in U(N),</math>
where <math>U_{ji}</math> is an element in the defining matrix representation of {{math|''U''(''N'')}}.
 
The energy levels of the system are
<math display="block"> E = \hbar \omega \left[(n_1 + \cdots + n_N) + {N\over 2}\right].</math>
<math display="block">n_i = 0, 1, 2, \dots \quad (\text{the energy level in dimension } i).</math>
 
As in the one-dimensional case, the energy is quantized. The ground state energy is {{math|''N''}} times the one-dimensional ground energy, as we would expect using the analogy to {{math|''N''}} independent one-dimensional oscillators. There is one further difference: in the one-dimensional case, each energy level corresponds to a unique quantum state. In {{math|''N''}}-dimensions, except for the ground state, the energy levels are ''degenerate'', meaning there are several states with the same energy.
 
The degeneracy can be calculated relatively easily.  As an example, consider the 3-dimensional case: Define {{math|1=''n'' = ''n''<sub>1</sub> + ''n''<sub>2</sub> + ''n''<sub>3</sub>}}. All states with the same {{math|''n''}} will have the same energy.  For a given {{math|''n''}}, we choose a particular {{math|''n''<sub>1</sub>}}. Then {{math|1=''n''<sub>2</sub> + ''n''<sub>3</sub> = ''n'' − ''n''<sub>1</sub>}}. There are {{math|''n'' − ''n''<sub>1</sub> + 1}} possible pairs {{math|{{mset|''n''<sub>2</sub>, ''n''<sub>3</sub>}}}}. {{math|''n''<sub>2</sub>}} can take on the values {{math|0}} to {{math|''n'' − ''n''<sub>1</sub>}}, and for each {{math|''n''<sub>2</sub>}} the value of {{math|''n''<sub>3</sub>}} is fixed. The degree of degeneracy therefore is:
<math display="block">g_n = \sum_{n_1=0}^n n - n_1 + 1 = \frac{(n+1)(n+2)}{2}</math>
Formula for general {{math|''N''}} and {{math|''n''}} [{{math|''g''<sub>''n''</sub>}} being the dimension of the symmetric irreducible {{math|''n''}}-th power representation of the unitary group {{math|''U''(''N'')}}]:
<math display="block">g_n = \binom{N+n-1}{n}</math>
The special case {{math|''N''}} = 3, given above, follows directly from this general equation.  This is however, only true for distinguishable particles, or one particle in {{math|''N''}} dimensions (as dimensions are distinguishable). For the case of {{math|''N''}} bosons in a one-dimension harmonic trap, the degeneracy scales as the number of ways to partition an integer {{math|''n''}} using integers less than or equal to {{math|''N''}}.
 
<math display="block">g_n = p(N_{-},n)</math>
 
This arises due to the constraint of putting {{math|''N''}} quanta into a state ket where <math display="inline">\sum_{k=0}^\infty k n_k = n  </math>   and <math display="inline"> \sum_{k=0}^\infty  n_k = N </math>, which are the same constraints as in integer partition.
 
===Example: 3D isotropic harmonic oscillator===
[[File:2D_Spherical_Harmonic_Orbitals.png|thumb|300px|right|Schrödinger 3D spherical harmonic orbital solutions in 2D density plots; the [[Mathematica]] source code that used for generating the plots is at the top]]
The Schrödinger equation for a particle in a spherically-symmetric three-dimensional harmonic oscillator can be solved explicitly by separation of variables; see [[Particle in a spherically symmetric potential#3D isotropic harmonic oscillator|this article]] for the present case. This procedure is analogous to the separation performed in the [[Hydrogen-like atom#Schrödinger equation in a spherically symmetric potential|hydrogen-like atom]] problem, but with a different [[Particle in a spherically symmetric potential|spherically symmetric potential]]
<math display="block">V(r) = {1\over 2} \mu \omega^2 r^2,</math>
where {{mvar|μ}} is the mass of the particle. Because {{mvar|m}} will be used below for the magnetic quantum number, mass is indicated by  {{mvar|μ}}, instead of {{mvar|m}}, as earlier in this article.


The solution reads<ref>[[Albert Messiah]], ''Quantum Mechanics'', 1967, North-Holland, Ch XII,  § 15, p 456.[https://archive.org/details/QuantumMechanicsVolumeI/page/n239 online]</ref>
===[[Taunt]]s===
<math display="block">\psi_{klm}(r,\theta,\phi) = N_{kl} r^{l}e^{-\nu r^2}L_k^{\left(l+{1\over 2}\right)}(2\nu r^2) Y_{lm}(\theta,\phi)</math>
*'''Up Taunt''': Stands upright, clasping its hands together before assuming a ninjutsu stance. The stance resembles one of its attack animations from the ''Pokémon'' series.
where
*'''Side Taunt''': Shakes head from side to side, causing its tongue to whip out in the same directions. Particles of saliva fly off with each whip.
:<math>N_{kl}=\sqrt{\sqrt{\frac{2\nu^3}{\pi }}\frac{2^{k+2l+3}\;k!\;\nu^l}{(2k+2l+1)!!}}~~</math> is a normalization constant; <math>\nu \equiv {\mu \omega \over 2 \hbar}~</math>;
*'''Down Taunt''': Poses with arms out and palms upward, and summons small sprays of water from them, which deal a small amount of damage.
:<math>{L_k}^{(l+{1\over 2})}(2\nu r^2)</math>  
<gallery>
are [[Laguerre polynomials#Generalized Laguerre polynomials|generalized Laguerre polynomials]]; The order {{mvar|k}}  of the polynomial is a non-negative integer;
SSBUGreninjaTaunt1.gif|Greninja's up taunt.
*<math>Y_{lm}(\theta,\phi)\,</math> is a [[spherical harmonics|spherical harmonic function]];
SSBUGreninjaTaunt2.gif|Greninja's side taunt.
*{{mvar|ħ}} is the reduced [[Planck constant]]: <math>\hbar\equiv\frac{h}{2\pi}~.</math>
SSBUGreninjaTaunt3.gif|Greninja's down taunt.
</gallery>


The energy eigenvalue is
===[[Idle Pose]]s===
<math display="block">E=\hbar \omega \left(2k + l + \frac{3}{2}\right) .</math>
*Crosses arms over its body, then separates them with a flourish.
The energy is usually described by the single [[quantum number]]
*Hunches over and assumes a ninjutsu stance.
<math display="block">n\equiv 2k+l  \,.</math>
<gallery>
SSBUGreninjaIdle1.gif|Greninja's first idle pose
SSBUGreninjaIdle2.gif|Greninja's second idle pose
</gallery>


Because {{mvar|k}} is a non-negative integer, for every even {{mvar|n}} we have {{math|1=''ℓ'' = 0, 2, …, ''n'' − 2, ''n''}} and for every odd {{mvar|n}}  we have {{math|1=''ℓ'' = 1, 3, …, ''n'' − 2, ''n''}} . The magnetic quantum number {{mvar|m}} is an integer satisfying {{math|−''ℓ'' ≤ ''m'' ≤ ''ℓ''}}, so for every {{mvar|n}} and ''ℓ'' there are 2''ℓ''&nbsp;+&nbsp;1 different [[quantum state]]s, labeled by {{mvar|m}} . Thus, the degeneracy at level {{mvar|n}} is
===[[Crowd cheer]]===
<math display="block">\sum_{l=\ldots,n-2,n} (2l+1) = {(n+1)(n+2)\over 2} \,,</math>
<div class="tabber">
where the sum starts from 0 or 1, according to whether {{mvar|n}} is even or odd.
<div class="tabbertab" title="English, Japanese/Chinese, Italian, Dutch, French">
This result is in accordance with the dimension formula above, and amounts to the dimensionality of a symmetric representation of {{math|SU(3)}},<ref>Fradkin, D. M. "Three-dimensional isotropic harmonic oscillator and SU3." ''American Journal of Physics'' '''33''' (3) (1965) 207–211.</ref> the relevant degeneracy group.
{| class="wikitable" border="1" cellpadding="4" cellspacing="1"
|-
!{{{name|}}}
!Cheer (English)
!Cheer (Japanese/Chinese)
!Cheer (Italian)
!Cheer (Dutch)
!Cheer (French)
|-
! scope="row"|Cheer
|[[File:Greninja Cheer English SSBU.ogg|center]]||[[File:Greninja Cheer Japanese SSBU.ogg|center]]||[[File:Greninja Cheer Italian SSBU.ogg|center]]||[[File:Greninja Cheer Dutch SSBU.ogg|center]]||{{NTSC}} [[File:Greninja Cheer French NTSC SSBU.ogg|center]] <br> {{PAL}} [[File:Greninja Cheer French PAL SSBU.ogg|center]]
|-
! scope="row"|Description
|Gre - ninja! || Ge - kkou -ga! || Gre - nin - ja! || Gre - ninja! || Am - phi - no - bi!
|}
</div>
<div class="tabbertab" title="German, Spanish, Russian, Korean">
{| class="wikitable" border="1" cellpadding="4" cellspacing="1"
|-
!{{{name|}}}
!Cheer (German)
!Cheer (Spanish)
!Cheer (Russian)
!Cheer (Korean)
|-
! scope="row"|Cheer
|[[File:Greninja Cheer German SSBU.ogg|center]]||{{NTSC}} [[File:Greninja Cheer Spanish NTSC SSBU.ogg|center]] <br> {{PAL}} [[File:Greninja Cheer Spanish PAL SSBU.ogg|center]]||[[File:Greninja Cheer Russian SSBU.ogg|center]]||[[File:Greninja Cheer Korean SSBU.ogg|center]]
|-
! scope="row"|Description
|Quaaaaa - jutsu! || Greninja! Greninja! Ya ya ya! || Gre - ninja! || Gae - gul - nin - ja!
|}
</div>
</div>


==Applications==
===[[Victory pose]]s===
===Harmonic oscillators lattice: phonons===
*'''Left:''' Does a few hand seals with splashing water, and then a ninja pose. It resembles one of its attack animations in [[bulbapedia:Pokémon X and Y|''Pokémon X'' and ''Y'']].
{{see also|Canonical quantization}}
*'''Up:''' Performs Double Team to briefly create three afterimages of itself.
*'''Right:''' Does a flip, lands in a spinning pose, and crosses its arms.
[[File:PokemonSeriesVictoryThemeUltimate.ogg|thumb|A small excerpt of the title theme of ''Pokémon Red, Blue, Yellow, and Green Versions'', a track which would go on to become the ''Pokémon'' main theme and the title theme for the entire series.]]
<gallery>
GreninjaVictoryPose1SSBU.gif
GreninjaVictoryPose2SSBU.gif
GreninjaVictoryPose3SSBU.gif
</gallery>


We can extend the notion of a harmonic oscillator to a one-dimensional lattice of many particles. Consider a one-dimensional quantum mechanical ''harmonic chain'' of ''N'' identical atoms. This is the simplest quantum mechanical model of a lattice, and we will see how [[phonon]]s arise from it. The formalism that we will develop for this model is readily generalizable to two and three dimensions.
==In competitive play==
In the early metagame, players quickly noticed that Greninja had been buffed from ''Smash 4'', with improved versatility and speed and, despite losing its [[footstool]] combos, gained a stronger combo game thanks to improved frame data on moves such as dash attack, up throw, down throw, and neutral air. Despite this, Greninja is not a very popular pick due to its high learning curve. Nevertheless, smashers such as {{Sm|Stroder}},  {{Sm|Venia}}, {{Sm|Jw}}, and {{Sm|Lea}} have proven that the character is a very viable pick, and Greninja has been solidified as a upper high-tier character.


As in the previous section, we denote the positions of the masses by  {{math|''x''<sub>1</sub>, ''x''<sub>2</sub>, …}}, as measured from their equilibrium positions (i.e. {{math|1=''x<sub>i</sub>'' = 0}} if the particle {{mvar|i}} is at its equilibrium position). In two or more dimensions, the {{math|''x<sub>i</sub>''}} are vector quantities. The [[Hamiltonian (quantum mechanics)|Hamiltonian]] for this system is
===Most historically significant players===
<!--This character has a ten player limit for this section. Before adding and/or removing a player, read these guidelines: https://www.ssbwiki.com/SmashWiki:Notability#%22Most_historically_significant_players%22_guidelines -->


<math display="block">\mathbf{H} = \sum_{i=1}^N {p_i^2 \over 2m} + {1\over 2} m \omega^2 \sum_{\{ij\} (nn)} (x_i - x_j)^2 \,,</math>
''Any number following the Smasher name indicates placement on the [[Fall 2019 PGRU]], which recognizes the official top 50 players in the world in [[Super Smash Bros. Ultimate]] from July 13th, 2019 to December 15th, 2019.''
where {{mvar|m}} is the (assumed uniform) mass of each atom, and  {{math|''x<sub>i</sub>''}} and  {{math|''p<sub>i</sub>''}} are the position and [[momentum]] operators for the ''i'' th atom and the sum is made over the nearest neighbors (nn).  However, it is customary to rewrite the Hamiltonian in terms of the [[normal modes]] of the [[wavevector]] rather than in terms of the particle coordinates so that one can work in the more convenient [[Fourier space]].


We introduce, then, a set of {{mvar|N}} "normal coordinates" {{math|''Q<sub>k</sub>''}}, defined as the [[discrete Fourier transform]]s of the {{mvar|x}}s, and {{mvar|N}} "conjugate momenta"  {{mvar|Π}} defined as the Fourier transforms of the {{mvar|p}}s,
''See also: [[:Category:Greninja professionals (SSBU)]]''
<math display="block">Q_k = {1\over\sqrt{N}} \sum_{l} e^{ikal} x_l</math>
<math display="block">\Pi_{k} = {1\over\sqrt{N}} \sum_{l}  e^{-ikal} p_l \,.</math>


The quantity {{math|''k<sub>n</sub>''}} will turn out to be the [[Wavenumber|wave number]] of the phonon, i.e. 2''π''  divided by the [[wavelength]]. It takes on quantized values, because the number of atoms is finite.
*{{Sm|Elexiao|France}} - One of the best Greninja players in Europe. Placed 1st at {{Trn|4 Seasons Tournament: Winter 2020}}, 2nd at {{Trn|SEL 4: Crêpes Strikes Back}}, 5th at {{Trn|VCA 2019}}, 7th at {{Trn|Valhalla III}}, and 9th at {{Trn|Ultimate Fighting Arena 2019}} with wins over players such as {{Sm|Oryon}}, {{Sm|Flow}}, and {{Sm|Tru4}}. Currently ranked 13th on the [[European Smash Rankings]].
*{{Sm|iStudying|Netherlands}} - One of the best Greninja players in Europe. Placed 1st at both {{Trn|The Ultimate Performance 3}} and {{Trn|Heroes of Dutch Comic Con Winter Edition}}, 9th at both {{Trn|Ultimate Fighting Arena 2019}} and {{Trn|Temple: Hermès Edition}}, and 13th at {{Trn|Valhalla III}} with wins over players such as {{Sm|Stroder Ame}}, {{Sm|quiK}}, and {{Sm|Space}}. Currently ranked 15th on the [[European Smash Rankings]].
*{{Sm|Jw|Canada}} - The best Greninja player in Canada. Placed 9th at {{Trn|Pound 2019}}, 13th at {{Trn|Shine 2019}}, 17th at both {{Trn|Get On My Level 2019}} and {{Trn|The Big House 9}}, and 33rd at {{Trn|Frostbite 2020}} with wins over players such as {{Sm|MkLeo}}, {{Sm|Mr. E}}, and {{Sm|Wishes}}. Currently ranked 1st on the [[Smash Canada Rankings Ultimate]].
*{{Sm|Lea|Japan}} (#21) - The best Greninja player in the world. Placed  5th at both {{Trn|Umebura SP 3}} and {{Trn|Umebura SP 6}}, 7th at both {{Trn|2GG: Kongo Saga}} and  {{Trn|Kagaribi 4}}, and 9th at {{Trn|Frostbite 2019}} with wins over players such as {{Sm|KEN}}, {{Sm|Raito}}, and {{Sm|Dabuz}}.
*{{Sm|Oisiitofu|Japan}} -  Placed 9th at both {{Trn|Sumabato SP 2}} and {{Trn|Maesuma TOP 1}}, 13th at {{Trn|Sumabato SP 12}}, and 17th at both {{Trn|KVOxTSB 2019}} and {{Trn|Sumabato SP 7}} with wins over players such as {{Sm|Zackray}}, {{Sm|Atelier}}, and {{Sm|Nishiya}}. Currently ranked 86th on the [[Japan Player Rankings]].
*{{Sm|Regerets|Philippines}} - The best Greninja player in the Philippines. Placed 3rd at {{Trn|Gamebookr's Mid-Year Smash Tournament}} and 7th at both {{Trn|Uprising 2019}} and {{Trn|REV Major 2019}} with wins over players such as {{Sm|Aluf}}, {{Sm|JJROCKETS}}, and {{Sm|PSI Force}}. Currently ranked 1st on the [[Filipino Power Rankings]].
*{{Sm|Somé|Japan}} - Placed 1st at {{Trn|TSC 11}}, 3rd at {{Trn|TSC 12}}, 7th at {{Trn|Sumabato SP 4}}, 9th at {{Trn|Umebura SP 6}}, and 13th at {{Trn|Umebura SP 4}} with wins over players such as {{Sm|Jagaimo}}, {{Sm|Etsuji}}, and {{Sm|HIKARU}}. Currently ranked 21st on the [[Japan Player Rankings]].
*{{Sm|Stroder|USA}} - One of the best Greninja players in the world. Placed 1st at {{Trn|Ascension VIII}}, 5th at {{Trn|Glitch 8 - Missingno}}, 9th at {{Trn|Mainstage}}, 13th at {{Trn|Shine 2019}}, and 25th at {{Trn|EVO 2019}} with wins over players such as {{Sm|Tweek}}, {{Sm|Maister}}, and {{Sm|ESAM}}. Formerly ranked 29th on the [[Spring 2019 PGRU]].
*{{Sm|Tarik|Germany}} - One of the best Greninja players in Europe. Placed 1st at {{Trn|Calyptus Cup X: Powwer Up}}, 2nd at {{Trn|Smashwick 4}}, 7th at {{Trn|Syndicate 2019}}, 9th at {{Trn|Ultimate Fighting Arena 2019}}, and 25th at {{Trn|Glitch 8 - Missingno}} with wins over players such as {{Sm|ESAM}}, {{Sm|MVD}}, and {{Sm|Chag}}. Ranked 14th on the [[European Smash Rankings]].
*{{Sm|Venia|USA}} -  One of the best Greninja players in the United States but is currently banned from several tournaments. Placed 3rd at both {{Trn|Player's Ball Ultimate}} and {{Trn|Return to Yoshi's Island}}, 25th at {{Trn|Let's Make Big Moves}}, and 33rd at both {{Trn|The Big House 9}} and {{Trn|GENESIS 7}} with wins over {{Sm|Tweek}}, {{Sm|Dabuz}}, and {{Sm|Mr. E}}. Currently ranked 2nd on the [[New York City Power Rankings#Super Smash Bros. Ultimate rankings|New York City Ultimate Power Rankings]].


This preserves the desired commutation relations in either real space or wave vector space
=={{SSBU|Classic Mode}}: Your Turn, Greninja!==
<math display="block"> \begin{align}  
[[File:SSBU Congratulations Greninja.png|thumb|Greninja's congratulations screen.]]
\left[x_l , p_m \right]&=i\hbar\delta_{l,m} \\
Greninja fights against characters that represent different types from the ''Pokémon'' games: for example, Charizard and Bowser represent the Fire type, while Mewtwo, Ness and Lucas represent the Psychic type.
\left[ Q_k , \Pi_{k'} \right] &={1\over N} \sum_{l,m} e^{ikal} e^{-ik'am}  [x_l , p_m ] \\
&= {i \hbar\over N} \sum_{m} e^{iam(k-k')} = i\hbar\delta_{k,k'} \\
\left[ Q_k , Q_{k'} \right] &= \left[ \Pi_k , \Pi_{k'} \right] = 0 ~.
\end{align}</math>


From the general result
{|class="wikitable" style="text-align:center"
<math display="block"> \begin{align}
!Round!!Opponent!!Stage!!Music!!Notes
\sum_{l}x_l x_{l+m}&={1\over N}\sum_{kk'}Q_k Q_{k'}\sum_{l} e^{ial\left(k+k'\right)}e^{iamk'}= \sum_{k}Q_k Q_{-k}e^{iamk} \\
|-
\sum_{l}{p_l}^2 &= \sum_{k}\Pi_k \Pi_{-k}   ~,
|1||{{CharHead|Charizard|SSBU|hsize=20px}} and {{CharHead|Bowser|SSBU|hsize=20px}}||[[Pokémon Stadium]]||''{{SSBUMusicLink|Pokémon|Battle! (Elite Four) / Battle! (Solgaleo/Lunala)}}''||Represents Fire-type. Charizard's {{SSBU|Pokémon Trainer}} is absent.
\end{align}</math>
|-
it is easy to show, through elementary trigonometry, that the potential energy term is
|2||{{CharHead|Pikachu|SSBU|hsize=20px}}, {{CharHead|Pichu|SSBU|hsize=20px}}, and {{CharHead|Zero Suit Samus|SSBU|hsize=20px}}||[[Pokémon Stadium 2]]||''{{SSBUMusicLink|Pokémon|Battle! (Steven)}}''||Represents Electric-type.
<math display="block"> {1\over 2} m \omega^2 \sum_{j} (x_j - x_{j+1})^2= {1\over 2} m \omega^2\sum_{k}Q_k Q_{-k}(2-e^{ika}-e^{-ika})= {1\over 2} m \sum_{k}{\omega_k}^2Q_k Q_{-k} ~ ,</math>
|-
where
|3||{{CharHead|Lucario|SSBU|hsize=20px}}, {{CharHead|Ryu|SSBU|hsize=20px}}, and {{CharHead|Ken|SSBU|hsize=20px}}||Pokémon Stadium||''{{SSBUMusicLink|Pokémon|Battle! (Reshiram / Zekrom)}}''||Represents Fighting-type.
<math display="block">\omega_k = \sqrt{2 \omega^2 (1 - \cos(ka))} ~.</math>
|-
|4||{{CharHead|Ivysaur|SSBU|hsize=20px}}||Pokémon Stadium||''{{SSBUMusicLink|Pokémon|Battle! (Gladion)}}''||Represents Grass-type. Ivysaur's Pokémon Trainer is absent.
|-
|5||{{CharHead|Mewtwo|SSBU|hsize=20px}}, {{CharHead|Ness|SSBU|hsize=20px}}, and {{CharHead|Lucas|SSBU|hsize=20px}}||Pokémon Stadium 2||''{{SSBUMusicLink|Pokémon|Battle! (Dialga/Palkia) / Spear Pillar}}''||Represents Psychic-type.
|-
|6||{{CharHead|Squirtle|SSBU|hsize=20px}} and {{Head|Greninja|g=SSBU|s=20px|cl=Black}} Greninja||[[Kalos Pokémon League]]||''{{SSBUMusicLink|Pokémon|Battle! (Champion) - Pokémon X / Pokémon Y}}''||Represents Water-type. Squirtle's Pokémon Trainer is absent.  The CPU will be the {{Head|Greninja|g=SSBU|s=20px}} default Greninja if the player chooses the black costume.
|-
|colspan="5"|[[Bonus Stage]]
|-
|Final||{{SSBU|Master Hand}}||{{SSBU|Final Destination}}||''{{SSBUMusicLink|Super Smash Bros.|Master Hand}}'' <small>(Less than 7.0 intensity)</small><br>''{{SSBUMusicLink|Super Smash Bros.|Master Hand / Crazy Hand}}'' <small>(Intensity 7.0 or higher)</small>||On intensity 7.0 and higher, {{SSBU|Crazy Hand}} fights alongside Master Hand.
|}


The Hamiltonian may be written in wave vector space as
Note: All rounds except the sixth round take place on Pokémon Stadium and Pokémon Stadium 2. If applicable, each stage will also shift to their appropriately-typed form at the earliest possible opportunity. (The stages remain in their default form in rounds 3 and 5, as none of the stages have Psychic or Fighting-themed forms.)
<math display="block">\mathbf{H} = {1\over {2m}}\sum_k \left(
{ \Pi_k\Pi_{-k} } + m^2 \omega_k^2 Q_k Q_{-k}
\right) ~.</math>


Note that the couplings between the position variables have been transformed away; if the {{mvar|Q}}s and {{mvar| Π}}s were [[Hermitian operator|hermitian]] (which they are not), the transformed Hamiltonian would describe {{mvar|N}} ''uncoupled'' harmonic oscillators.
[[Credits]] roll after completing Classic Mode. Completing it as Greninja has ''{{SSBUMusicLink|Pokémon|Battle! (Trainer Battle) - Pokémon X / Pokémon Y}}'' accompany the credits.
{{clr}}


The form of the quantization depends on the choice of boundary conditions; for simplicity, we impose ''periodic'' boundary conditions, defining the {{math|(''N'' + 1)}}-th atom as equivalent to the first atom. Physically, this corresponds to joining the chain at its ends. The resulting quantization is
==Role in [[World of Light]]==
[[File:WoL-50Greninja.jpg|thumb|Finding Greninja in World of Light|left]]
Greninja was among the fighters that were summoned to fight the army of [[Master Hand]]s.


<math display="block">k=k_n = {2n\pi \over Na}
During the opening cutscene, Greninja was present on the cliffside when [[Galeem]] unleashed his beams of light. Greninja leaped into the air to avoid one of the beams, which hit {{SSBU|Lucario}} instead. Greninja was hit shortly after and vaporized, getting imprisoned by Galeem afterward along with the other fighters, sans {{SSBU|Kirby}}. A puppet fighter cloned from Greninja is later seen alongside ones cloned from {{SSBU|Fox}}, {{SSBU|Samus}}, {{SSBU|Link}} and other fighters.
\quad \hbox{for}\ n = 0, \pm1, \pm2, \ldots , \pm {N \over 2}. </math>


The upper bound to {{mvar|n}} comes from the minimum wavelength, which is twice the lattice spacing {{mvar|a}}, as discussed above.
Greninja was one of the many fighters that fell under [[Dharkon]]'s control upon Galeem's first defeat, and it can be found in the [[Mysterious Dimension]] at [[The Dark Realm]]. It can be seen impeding the path, making it an obligatory unlock.


The harmonic oscillator eigenvalues or energy levels for the mode {{math|''ω<sub>k</sub>''}} are
Greninja is later seen among several other fighters, making their last stand against Galeem and Dharkon. It also shows up in the bad ending where Galeem emerges victorious against Dharkon, witnessing Galeem engulf the world in light.
<math display="block">E_n = \left({1\over2}+n\right)\hbar\omega_k  \quad\hbox{for}\quad n=0,1,2,3,\ldots</math>
{{clrl}}


If we ignore the [[zero-point energy]] then the levels are evenly spaced at
===Fighter Battle===
<math display="block">\hbar\omega,\, 2\hbar\omega,\, 3\hbar\omega,\, \ldots  </math>
{|class="wikitable" style="width:100%;"
|-
!style="width:5%;"|No.
!style="width:5%;"|Image
!Name
!Type
!Power
!Stage
!Music
|-
|50
|[[File:Greninja SSBU.png|center|64x64px]]
|Greninja
|{{SpiritType|Shield}} <center>{{color|#18aef5|Shield}}</center>
|10,600
|[[Kalos Pokémon League]] ([[Ω form]])
|''{{SSBUMusicLink|Pokémon|Battle! (Trainer Battle) - Pokémon X / Pokémon Y}}''
|}
{{clear}}


So an '''exact''' amount of [[energy]] {{math|''ħω''}}, must be supplied to the harmonic oscillator lattice to push it to the next energy level. In analogy to the [[photon]] case when the [[electromagnetic field]] is quantised, the quantum of vibrational energy is called a [[phonon]].
==[[Spirit]]==
Greninja's fighter spirit can be obtained by completing {{SSBU|Classic Mode}}. It is also available periodically for purchase in the shop for 300 Gold, but only after Greninja has been unlocked. Unlocking Greninja in World of Light allows the player to preview the spirit below in the Spirit List under the name "???". As a fighter spirit, it cannot be used in Spirit Battles and is purely aesthetic. Its fighter spirit has an alternate version that replaces it with its artwork in ''Ultimate''.


All quantum systems show wave-like and particle-like properties. The particle-like properties of the phonon are best understood using the methods of [[second quantization]] and operator techniques described elsewhere.<ref name="Mahan">{{cite book| last=Mahan |first=GD |title=Many particle physics|publisher= Springer|location=New York | isbn=978-0306463389 |year=1981}}</ref>
<center>
<gallery>
SSBU spirit Greninja.png|418. '''''Greninja'''''
</gallery>
</center>


In the continuum limit, ''a''→0, ''N''→∞, while ''Na'' is held fixed. The canonical coordinates ''Q<sub>k</sub>'' devolve to the decoupled momentum modes of a scalar field, <math>\phi_k</math>, whilst the location index {{mvar|i}} (''not the displacement dynamical variable'') becomes the ''parameter {{mvar|x}} argument of the scalar field, <math>\phi (x,t)</math>.
==In Spirit battles==
===As the main opponent===
{|class="wikitable sortable" style="width:100%;"
! colspan=4|Spirit
! colspan=7|Battle parameters
! colspan=1|Inspiration
|-
! style="width:5%;"|No.
! style="width:5%;"|Image
! Name
! Series
! Enemy Fighter(s)
! style="width:5%;"|Type
! style="width:5%;"|Power
! Stage
! Rules
! Conditions
! Music
! Character
|-
|154
|{{SpiritTableName|Winky|size=64}}
|''Donkey Kong'' Series
|•{{SSBU|Greninja}} {{Head|Greninja|g=SSBU|s=20px|cl=Green}}
|{{SpiritType|Attack}}
|1,700
|[[Mushroom Kingdom U]]
|N/A
|•The enemy deals damage when falling<br>•The enemy has increased jump power
|{{SSBUMusicLink|Donkey Kong|Jungle Level (Brawl)}}
|
|-
|199
|{{SpiritTableName|Zora|size=64}}
|''The Legend of Zelda'' Series
|•{{SSBU|Greninja}} {{Head|Greninja|g=SSBU|s=20px|cl=Violet}}
|{{SpiritType|Shield}}
|1,800
|[[Great Bay]]
|N/A
|•The enemy's neutral special has increased power
|{{SSBUMusicLink|The Legend of Zelda|Ocarina of Time Medley}}
|
|-
|385
|{{SpiritTableName|Slippy Toad|link=y|size=64}}
|''Star Fox'' Series
|•{{SSBU|Greninja}} {{Head|Greninja|g=SSBU|s=20px|cl=Green}}<br>•{{SSBU|Fox}} {{Head|Fox|g=SSBU|s=20px|cl=Black}}
|{{SpiritType|Shield}}
|9,600
|[[Frigate Orpheon]] (hazards off)
|N/A
|•Defeat the main fighter to win<br>•Timed battle (1:30)<br>•The enemy tends to avoid conflict
|{{SSBUMusicLink|Star Fox|Corneria - Star Fox}}
|
|-
|482
|{{SpiritTableName|Raikou, Entei, & Suicune|customname=[[Raikou]], [[Entei]], & [[Suicune]]|size=64}}
|''Pokémon'' Series
|•{{SSBU|Greninja}} {{Head|Greninja|g=SSBU|s=20px|cl=Violet}}<br>•{{SSBU|Incineroar}} {{Head|Incineroar|g=SSBU|s=20px|cl=White}}<br>•{{SSBU|Pikachu}} {{Head|Pikachu|g=SSBU|s=20px|cl=Libre}}
|{{SpiritType|Shield}}
|9,900
|[[Suzaku Castle]]
|•Hazard: Lava Floor
|•The floor is lava
|{{SSBUMusicLink|Pokémon|Pokémon Red / Pokémon Blue Medley}}
|Suicune
|-
|516
|{{SpiritTableName|Darkrai|link=y|size=64}}
|''Pokémon'' Series
|•{{SSBU|Greninja}} {{Head|Greninja|g=SSBU|s=20px|cl=Black}}
|{{SpiritType|Shield}}
|9,900
|[[Luigi's Mansion]] ([[Ω form]])
|•Item: [[Black Hole]]<br>•Hazard: Slumber Floor
|•The floor is sleep-inducing<br>•Only certain Pokémon will emerge from Poké Balls (Darkrai)
|{{SSBUMusicLink|Pokémon|Battle! (Team Galactic)}}
|
|-
|770
|{{SpiritTableName|Metal Gear RAY|size=64}}
|''Metal Gear Solid'' Series
|•Metal {{SSBU|Greninja}} {{Head|Greninja|g=SSBU|s=20px|cl=Grey}} (140 HP)
|{{SpiritType|Grab}}
|4,200
|[[Shadow Moses Island]]
|•Item: Exploding Types
|•[[Stamina battle]]<br>•Explosion attacks aren't as effective against the enemy<br>•The enemy is metal
|{{SSBUMusicLink|Metal Gear|Yell "Dead Cell"}}
|
|-
|893
|{{SpiritTableName|Shadow Man|size=64}}
|''Mega Man'' Series
|•{{SSBU|Greninja}} {{Head|Greninja|g=SSBU|s=20px|cl=Purple}}×3 (60 HP)
|{{SpiritType|Shield}}
|3,500
|[[Norfair]] ([[Battlefield form]])
|N/A
|•The enemy's neutral special has increased power<br>•[[Stamina battle]]<br>•The enemy favors neutral specials
|{{SSBUMusicLink|Mega Man|Shadow Man Stage}}
|
|-
|1,014
|{{SpiritTableName|Luka|size=64}}
|''Bayonetta'' Series
|•{{SSBU|Greninja}} {{Head|Greninja|g=SSBU|s=20px|cl=Black}}
|{{SpiritType|Shield}}
|3,800
|[[New Donk City Hall]]
|•Temporary Invincibility
|•The enemy becomes temporarily invincible when badly damaged
|{{SSBUMusicLink|Bayonetta|Riders Of The Light}}
|
|-
|1,048
|{{SpiritTableName|Octoling Octopus|size=64}}
|''Splatoon'' Series
|•{{SSBU|Greninja}} Team {{Head|Greninja|g=SSBU|s=20px|cl=Pink}}×4
|{{SpiritType|Shield}}
|3,900
|[[Moray Towers]]
|N/A
|•Timed battle (2:00)
|{{SSBUMusicLink|Splatoon|Octoweaponry}}
|
|-
|1,143
|{{SpiritTableName|Frog & Snake|customname=[[Sablé Prince|Frog & Snake]]|size=64}}
|''Kaeru no Tame ni Kane wa Naru''
|•{{SSBU|Greninja}} {{Head|Greninja|g=SSBU|s=20px|cl=Green}}<br>•{{SSBU|King K. Rool}} {{Head|King K. Rool|g=SSBU|s=20px|cl=Blue}}
|{{SpiritType|Shield}}
|3,600
|[[Dream Land GB]] (Castle Lololo interior)
|•Assist Trophy Enemies ([[Sablé Prince]])
|•Hostile assist trophies will appear
|{{SSBUMusicLink|Kirby|Kirby Retro Medley}} (Castle Lololo)
|Frog
|-
|rowspan="2"|1,291
|{{SpiritTableName|Ninjara|link=y|size=64|dlcalt=y}}
|rowspan="2"|''ARMS''
|•{{SSBU|Greninja}} {{Head|Greninja|g=SSBU|s=20px|cl=Green}}
|rowspan="2"|{{SpiritType|Grab}}
|rowspan="2"|3,600
|rowspan="2"|[[Suzaku Castle]]
|rowspan="2"|•Item: [[Boomerang]]
|rowspan="2"|•The enemy has increased move speed
|rowspan="2"|{{SSBUMusicLink|ARMS|Ninja College}}
|rowspan="2"|
|-
|style="background-color:#EEE;"|•{{SSBU|Mii Brawler}} {{Head|Mii Brawler|g=SSBU|s=20px}} (Moveset [[Flashing Mach Punch|2]][[Suplex|3]][[Soaring Axe Kick|1]][[Counter Throw|3]], Ninjara Wig, Ninjara Outfit)<ref group="SB" name="DLC"/>
|}


===Molecular vibrations===
<references group="SB">
{{main|Molecular vibration}}
<ref name="DLC">This alternative occurs when the corresponding DLC has been purchased and downloaded.</ref>
* The vibrations of a [[diatomic molecule]] are an example of a two-body version of the quantum harmonic oscillator. In this case, the angular frequency is given by <math display="block">\omega = \sqrt{\frac{k}{\mu}} </math> where <math>\mu = \frac{m_1 m_2}{m_1 + m_2}</math> is the [[reduced mass]] and <math>m_1</math> and <math>m_2</math> are the masses of the two atoms.<ref>{{Cite web | title=Quantum Harmonic Oscillator | website=Hyperphysics | access-date=24 September 2009 | url=http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/hosc.html}}</ref>
</references>
* The [[Hooke's atom]] is a simple model of the [[helium]] atom using the quantum harmonic oscillator.
* Modelling phonons, as discussed above.
* A charge <math>q</math> with mass <math>m</math> in a uniform magnetic field <math>\mathbf{B}</math> is an example of a one-dimensional quantum harmonic oscillator: [[Landau quantization]].


==See also==
==[[Alternate costume (SSBU)#Greninja|Alternate costumes]]==
{{Div col}}
{|style="margin:1em auto 1em auto;text-align:center"
*[[Quantum pendulum]]
|-
*[[Quantum machine]]
|colspan=8|[[File:Greninja Palette (SSBU).png|link=Alternate costume (SSBU)#Greninja|1000px]]
*[[Gas in a harmonic trap]]
|-
*[[Creation and annihilation operators]]
|{{Head|Greninja|g=SSBU|s=50px}}
*[[Coherent state]]
|{{Head|Greninja|g=SSBU|s=50px|cl=Red}}
*[[Morse potential]]
|{{Head|Greninja|g=SSBU|s=50px|cl=Pink}}
*[[Bertrand's theorem]]
|{{Head|Greninja|g=SSBU|s=50px|cl=Black}}
*[[Mehler kernel]]
|{{Head|Greninja|g=SSBU|s=50px|cl=Violet}}
*[[Molecular vibration#Quantum mechanics|Molecular vibration]]
|{{Head|Greninja|g=SSBU|s=50px|cl=Green}}
{{Div col end}}
|{{Head|Greninja|g=SSBU|s=50px|cl=Grey}}
|{{Head|Greninja|g=SSBU|s=50px|cl=Purple}}
|}


==References==
==Gallery==
{{Reflist}}
<gallery>
Pokémon Smash Bros.png|Artwork of all playable Pokémon characters and Poké Ball Pokémon, as posted by the official Pokémon Twitter account.
SSBU Greninja Number.png|Greninja's fighter card.
Greninja unlock notice SSBU.jpg|Greninja's unlock notice.
SSBUWebsiteGreninja1.jpg|Greninja coming to a halt on [[Kalos Pokémon League]].
SSBUWebsiteGreninja2.jpg|Charging [[Water Shuriken]] next to {{SSBU|Ryu}} on [[Suzaku Castle]].
SSBUWebsiteGreninja3.jpg|Jumping on {{SSBU|Battlefield}}.
SSBUWebsiteGreninja4.jpg|Performing its neutral aerial with [[Leviathan]] on [[Midgar]].
SSBUWebsiteGreninja5.jpg|With its [[Substitute|Substitute Doll]] on [[Wuhu Island]] after [[tripping]].
SSBUWebsiteGreninja6.jpg|Performing [[Shadow Sneak]] on [[Luigi's Mansion]].
SSBUWebsiteLucario3.jpg|Struck by {{SSBU|Lucario}} on [[Pokémon Stadium 2]].
</gallery>


==External links==
===Fighter Showcase Video===
*[http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/hosc.html Quantum Harmonic Oscillator]
{{#widget:YouTube|id=rMCn8NuATaE}}
*[http://behindtheguesses.blogspot.com/2009/03/quantum-harmonic-oscillator-ladder.html Rationale for choosing the ladder operators]
*[http://www.brummerblogs.com/curvature/3d-harmonic-oscillator-eigenfunctions/  Live 3D intensity plots of quantum harmonic oscillator]
*[http://ltl.tkk.fi/~ethuneb/courses/monqo.pdf Driven and damped quantum harmonic oscillator (lecture notes of course "quantum optics in electric circuits")]


{{Use dmy dates|date=August 2019}}
==Trivia==
*In the ''Pokémon'' series, Ash-Greninja is only obtainable as a male. The fact that Greninja transforms into Ash-Greninja for its [[Final Smash]], [[Secret Ninja Attack]], implies that Greninja is a male in ''Ultimate''.
*Greninja's new character portrait resembles its [[air dodge]] animation.
**It also resembles {{SSB4|Fox}}'s character portrait from ''Super Smash Bros. 4'' but with the arm and leg positions mirrored.
*Greninja's fighter number, 50, is the same as the number of its [[mariowiki:Costume Mario|costume]] in ''Super Mario Maker''. It shares this distinction with {{SSBU|Inkling}}.
*Greninja, {{SSBU|Ivysaur}}, {{SSBU|Olimar}}, {{SSBU|Little Mac}}, {{SSBU|Ryu}} and {{SSBU|Ken}} are the only characters to never appear as minions in any Spirit battles.
*Alongside {{SSBU|Luigi}}, Greninja is one of two characters in ''Ultimate'' with a taunt that cannot be cancelled, due to the fact that their non-cancelable taunts have hitboxes.
**Strangely, this does not apply for {{SSBU|Snake}} and {{SSBU|Kazuya}}'s taunts that have damaging hitboxes
**Greninja and Luigi are also the only two characters whose Classic Mode titles feature their names.
*Greninja can also be unlocked immediately after clearing Classic Mode as Sheik, referencing their ninja-like traits and movements.
*Greninja appears slightly tilted in its [[damage meter]] compared to its character artwork. This distinction is shared with fellow ''Pokémon'' series character {{SSBU|Incineroar}}.
**Coincidentally, both are final evolutions of starter Pokémon and both have Dark as their secondary type.
**Both are also found and unlocked in the Dark Realm in World of Light.
*Incineroar and {{SSBU|Jigglypuff}} are the only Pokémon that are not encountered in Greninja's Classic Mode route.
*Oddly, Greninja does not vanish when performing a directional [[air dodge]] despite the sound effects playing. It shares this oddity with {{SSBU|Rosalina & Luma}} and {{SSBU|Palutena}}.
*In ''Ultimate'', Greninja has a weight of 88, which almost matches its weight in ''Pokémon'' (in pounds), being 88.2 lbs.


{{DEFAULTSORT:Quantum Harmonic Oscillator}}
{{SSBUCharacters}}
[[Category:Quantum models]]
{{Pokémon universe}}
[[Category:Quantum mechanics]]
[[Category:Greninja (SSBU)| ]]
[[Category:Oscillators]]
[[Category:Pokémon (SSBU)]]
[[Category:Spirits]]
[[es:Greninja (SSBU)]]

Revision as of 11:02, February 9, 2022

This article is about Greninja's appearance in Super Smash Bros. Ultimate. For the character in other contexts, see Greninja.
Greninja
in Super Smash Bros. Ultimate
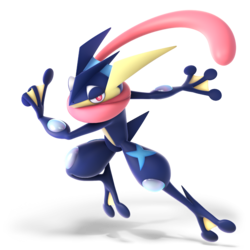
Greninja SSBU.png
PokemonSymbol.svg
Universe Pokémon
Other playable appearance in SSB4


Availability Unlockable
Final Smash Secret Ninja Attack
GreninjaHeadSSBU.png

Greninja (ゲッコウガ, Gekkouga) is a playable character in Super Smash Bros. Ultimate. It was officially revealed on June 12th, 2018 alongside Mr. Game & Watch and the rest of the returning roster. Greninja is classified as Fighter #50.

Billy Bob Thompson, Yūji Ueda, Frédéric Clou and Benedikt Gutjan's portrayals of Greninja from Super Smash Bros. 4 were repurposed for the English, Japanese, French and German versions of Ultimate, respectively.

How to unlock

Complete one of the following:

Greninja must then be defeated on Kalos Pokémon League (the Ω form is used in World of Light).

Attributes

Greninja, true to being a ninja-themed character, has very strong mobility; it has the 8th fastest run speed, the 10th fastest air speed, is tied for the 9th fastest falling (and fast falling) speed, the 2nd highest gravity, and possesses the 2nd highest jump height overall. However, unlike most characters who boast similar mobility (such as Sheik), Greninja boasts a surprising amount of KO options, good range on plenty of its attacks, and KO throws.

One of Greninja's most notable traits is its high mobility which complements its grounded moveset. Greninja's dash attack comes out on frame 7 and has very low ending lag, as well as the ability to cross upon shields. Its knockback angle allows for many true follow-ups and strings over a large range of percents. Its neutral jab attack comes out on frame 3, making it a good grounded combo breaker. It can also lock, which gives Greninja access to potent punishes from opponents missing techs. Its down tilt is an excellent combo starter due to its low startup, ending lag and vertical launch angle. Greninja's up tilt is a frame 9 disjointed hitbox that acts well as an anti-air and can also be a combo starter. Its smash attacks are also reliable in their own right; its forward smash is quick for its range and power, down smash is an excellent punishment option for ledge regrabs, as well as sending at a low angle, and up smash is a potent combo finisher.

Greninja also has a very strong air game due to its aforementioned air speed and jump height. Greninja's aerials are reliable for multiple situations and all have low landing lag (except for down aerial, at 30 frames). Its neutral aerial is a decent low percent combo starter due to it having incredibly low landing lag and a good launch angle. It can also KO at high percentages. Its forward aerial acts as a combo finisher from its combo starters and can KO moderately early. Forward aerial's low landing lag and disjointed nature also make it safe on shield in many situations when spaced correctly. Its up aerial is a great juggling option with low all-around lag and boasting good KO potential near the upper blast line. Greninja can also utilize its multihits to drag down opponents to create tech chase and jab lock situations. Its back aerial is a very fast follow up or offstage edgeguarding option. Down aerial can be used as a mix up to return to the stage from far above, as well as perform surprise combos on hit with both its meteor smash and sourspot hitbox.

Greninja's grab game is overall very effective, due to its grabs being among the longest ranges of any non-tether grab in the game. Its forward, up, and back throws can KO at high percentages. Down throw acts as a middle percent combo starter, as well as a strong DI mix up, especially at higher percentages at ledge as a 50/50 between DI in and out in conjunction with forward throw. Up throw acts as a versatile combo starter that can lead to juggling situations. Because of this, Greninja has plenty of options off of a grab, as not one of its throws could be considered useless.

Finally, Greninja's special moves are effective in various situations. Water Shuriken acts as a versatile zoning tool, as well as a high-percentage KO option when fully charged. At low-to-mid percents, it is also a combo starter, allowing Greninja to rush down its opponent and follow up with any aerial attack or an up smash. Shadow Sneak works as an effective recovery mix up, as well as a potent KO move from a good read or pseudo-combo finisher. Despite lacking an offensive hitbox, Hydro Pump is a good recovery move for its long distance, and can be used for gimping recoveries due to having windbox properties. Substitute is a counterattack with the unique attribute of being able to be aimed in one of 8 different directions upon a successful counter. These angled follow ups allow for Greninja to gain pseudo-follow ups as well as KO earlier by picking the optimal angle in regards to stage positioning.

Like all characters, Greninja is flawed in many ways. One of Greninja's primary flaws is its inability to break out of disadvantage state. While not as bad as the previous game, Greninja still has difficulties escaping combos due to its fast falling speed and its aerials still having relatively high startup. This can sometimes be alleviated with its back or down aerials, but both are not very effective due to back aerial's almost entirely horizontal hitboxes and down aerial's landing lag. Another option is aerial Water Shuriken, which stalls Greninja in the air and can be used as a landing mix up, as well as Hydro Pump landing mix ups.

Greninja's biggest weakness however, is its terrible out of shield game, which is arguably the worst of the entire cast. Because of its high short hop, its aerials slow startup, and lacking a fast grab (although it has good range), Greninja lacks an effective out of shield option faster than frame 14. While its back aerial is fairly quick at frame 5 (making it frame 8 out of shield), it is unable to hit opponents in front of Greninja and is very inconsistent at hitting opponents behind Greninja due to its high short hop. Jumping or rolling out of shield are potential options to reset neutral, but they are very predictable and easily read. Thus, when Greninja is pinned down in shield, it has difficulty escaping the situation without being heavily punished. Combined with its vulnerability to combos, this gives it an atrocious defensive game.

Altogether, Greninja's playstyle requires players to think like an actual ninja: utilizing Greninja's superb mobility and fast attacks to rush down opponents, saving the slower attacks for potential mixups, mindgames and surprise KO options, and remaining unpredictable to prevent being trapped into disadvantageous positions.

Changes from Super Smash Bros. 4

Greninja has been greatly buffed from Smash 4 to Ultimate. Its playstyle's traits have been further improved in the transition, while the general engine changes benefit said playstyle.

Most of the universal changes notably benefit Greninja. As with all other characters in the game, Greninja's already quick mobility is faster like most characters, which benefits its hit-and-run playstyle, allowing Greninja to close in the distance and escape to reset the neutral game much more easily. The ability to run cancel into any ground move allows Greninja to further exploit its amazing ground mobility, allowing for easier setups into its combo starters, such as up and down tilt and dash attack. Furthermore, the reduced landing lag on Greninja's aerial attacks gives it an easier time landing, while the universal 3-frame jumpsquat improves Greninja's ground-to-air potential. The implementation of spot dodge canceling improves its potential punish game, due to its wide variety of combo starters and fast frame data. Finally, the changes to air dodge mechanics slightly improve its previously below average edgeguarding game.

Aside from the universal changes, Greninja has also received notable direct buffs. The biggest ones were to its grab game: its standing grab is faster and its pummel, previously one of the worst in Smash 4, deals less damage but is significantly faster, which allows Greninja to deal much more damage before throwing the opponent. Greninja's forward throw has higher knockback, allowing it to KO in an emergency, as with up throw. Its up and down throws also have better combo and juggling potential due to the universal changes to mobility - down throw notably now allows for potential KO confirms into forward and back aerial. Other buffs include Water Shuriken having more range, improving Greninja's camping ability. Greninja now has a new down tilt that has lower ending lag and sends at more favorable angles, and its dash attack sends at a higher angle, further improving Greninja's combo game. Greninja's KO power has also been buffed, with forward smash and forward aerial receiving higher knockback, up smash connecting better into its second hit, and down smash having faster startup. Lastly, Substitute now slows opponents down and offers Greninja intangibility during all of its attack variations, bringing it in line with other counterattacks.

On the other hand, Greninja is not without its nerfs. Notably, the ability to tech footstools has made footstool combos harder to pull off, which hinders Greninja's combo ability (specifically from its down aerial); however, this nerf is alleviated by Greninja's buffed combo game, due to other universal changes that impact it more positively. Substitute's attack variants are all weaker while also being more laggy overall, which compensates for the attack's new intangibility. In exchange for its buffed mobility, Greninja is now lighter, which brings it slightly more in-line with other combo-centric and/or hit-and-run characters, while not compensating much for its vulnerability to combos.

As a result of receiving multiple buffs with relatively few nerfs, Greninja has improved significantly from Smash 4, and has retained its status as a viable character in Ultimate, with above average representation and some strong results in competitive play thanks to smashers such as iStudying, Jw, Lea, Somé, and Stroder. Because of this, Greninja is considered as a high or even top-tier character by many professional players.

Aesthetics

  • Change Greninja's model features a slightly more subdued color scheme, more closely resembling its appearance in recent mainline Pokémon games. Its body and tongue appear to have a glossy, wet sheen. The textures on Greninja's tongue have also been adjusted.
  • Change Greninja is slightly more expressive, squinting akin to how it does in the Pokémon anime in a few of his animations.
  • Change Every move that once used water katanas now uses water kunai, similar to when Ash's Greninja uses Cut in the Pokémon anime.
  • Change Greninja's tongue has less physics-based movement than the previous game.
  • Change Greninja has altered animations for its sidestep, roll, and airdodge animations; it now disappears in a small whirlwind with leaves scattering, similarly to when Substitute is successful.
  • Change Greninja's victory pose where it flips in the air and lands with its arms crossed has been altered: the camera doesn't move as much, causing Greninja's body to face away from the camera.

Attributes

  • Buff Like all characters, Greninja's jumpsquat animation takes 3 frames to complete (down from 4).
  • Buff Greninja walks faster (1.43 → 1.502).
  • Buff Greninja dashes faster (2.08 → 2.288).
    • Buff Its initial dash is significantly faster (1.6 → 2.178).
  • Buff Greninja's air speed is faster (1.18 → 1.239).
  • Nerf Greninja is lighter (94 → 88), worsening its survivability.
  • Buff Greninja's traction is higher (0.045 → 0.087).
  • Buff Forward roll has less ending lag (FAF 30 → 29).
  • Buff Back roll grants more intangibility (frames 4-14 → 4-15).
  • Nerf Back roll has more ending lag (FAF 33 → 34).
  • Buff Spot dodge has less ending lag (FAF 26 → 25).
  • Nerf Spot dodge has more startup with less intangibility (frames 2-16 → 3-16).
  • Buff Air dodge grants more intangibility (frames 2-26 → 2-27).
  • Nerf Air dodge has significantly more ending lag (FAF 32 → 42).
  • Nerf The changes to locking and the ability to tech aerial footstools hurts Greninja more than the rest of the cast, weakening notorious damage racking and KO setups it possessed in Smash 4.
  • Nerf The increased shieldstun, shield grab startup and shield drop lag further hinder Greninja's poor out of shield game, now being arguably the worst out of the cast, as unlike most other characters, all its options that can bypass shield drop lag are either too slow or, in the case of its back aerial, cannot hit most opponents on the ground.

Ground attacks

  • Neutral attack:
    • Buff The first two hits have lower knockback (hit 1: 30 base/30 scaling → 20 / 25/25/15/15; hit 2: 30 base/50 scaling → 20/ 25/25/20), and keep opponents on the ground (hit 1: 70°/60°/80° → 361°/361°/180°/361°; hit 2: 70°/60°/90° → 361°). This allows them to connect better and jab lock.
    • Nerf The first three hits have smaller hitboxes overall (hit 1: 3u/2.5u/3.5u → 2.0u/2.0u/2.2u/2.2u; hit 2: 3u/2.5u/4u → 2.5u/2.8u/3.0u; hit 3: 5u/3u/3u → 3u/3.4u/4u). This reduces their vertical range.
    • Buff The second hit deals more damage (1.6% → 2%).
    • Nerf The third hit deals less damage (3.5% → 3%), and thus less knockback.
    • Change The third hit uses stationary hitboxes rather than hitboxes connected to Greninja's arms.
    • Buff The infinite has faster startup (frame 6 → 4), a shorter gap between hits (4 frames → 3), and has reduced knockback scaling (40 → 10) while gaining a hitstun modifier of 2 on each hit, allowing it to connect much more reliably.
    • Buff The infinite has a lower hitlag multiplier (1× → 0.5×) and SDI multiplier (1.1× → 0.4×), making it harder to escape.
    • Change The infinite is comprised of one extended hitbox rather than two normal ones (size: 5.2u/6.2u → 5.5; Y/Z-offset: 7/7 → 7.5/7.5; Z-stretch: 13 → 14).
    • Change The infinite has gained a shieldstun multiplier of 4×. This allows it to lock opponents into their shields between each hit, and thus pressure them more effectively, but also allows them to cancel shieldstun and punish Greninja more easily if they shield 10 hits or more.
    • Change The infinite's finisher has three hitboxes instead of two, with different sizes (5.6u/6.6 → 4.2u/4.2u/4.8u) and positions (ID 0: 7 Y-offset/8 Z-offset → 7.5/9; ID 1: 7 Y-offset/16 Z-offset → 7.3/13 → ID 2: 7.5 Y-offset/16.5 Z-offset. This increases its horizontal range, but lowers its vertical range.
    • Change The infinite's finisher has reduced hitlag (3× → 2×).
  • Forward tilt:
    • Buff It deals more damage when angled (7.3% → 8.3%).
    • Change It has significantly altered knockback (angled up: 20/30/40 base / 110/90/70 scaling → 50 / 100/79/58; non-angled/angled down: 20/30/40 base / 110/90/70 scaling → 50 / 98/77/56).
      • Buff This improves its KO power if sweetspotted, especially when angled up, allowing it to KO middleweights at around 170% from center stage.
      • Nerf However, this hinders its KO power if sourspotted, and removes its ability to lock opponents at low percents.
  • Down tilt:
    • Change Greninja has a new down tilt: a downward hand sweep instead of a shin kick.
    • Buff It has less ending lag (FAF 27 → 23).
    • Buff It has altered knockback (60 base/40 scaling → 30/110). This slightly narrows its combo range at low percentages, but increases it from mid to higher ones, to the point it now allows for KO confirms at high percents.
    • Buff It launches opponents at a more upward angle (70° → 79°/77°/75°), further improving its combo potential at high percents.
    • Nerf It deals less damage (7% → 4%).
    • Nerf It has smaller hitboxes (4u/3.5u/3u → 3u/2.5u/3u), reducing its vertical range.
  • Dash attack:
    • Change The move has an altered animation with Greninja stopping halfway through the spin.
    • Buff It deals more damage (7% → 8%), with base knockback compensated (100 → 90).
    • Buff It has a longer hitbox duration (frames 7-10 → 7-11) and less ending lag (FAF 31 → 29).
    • Buff It sends at a higher angle (60° → 70°). Combined with its lower ending lag and base knockback, this improves its combo ability.
  • Forward smash:
    • Buff It deals more knockback (30 base/101 scaling → 35/104).
  • Up smash:
    • Buff The first hit has a new hitbox that only hits grounded opponents with significantly reduced knockback (30 base/120 scaling → 20/10) and SDI multiplier (1× → 0.5×), whereas the previous hitbox can now only hit aerial opponents and has reduced knockback scaling (120 → 90). This makes the first hit connect more consistently into the second hit, no longer failing against opponents on platforms above Greninja.
  • Down smash:
    • Buff The move has much less startup lag (frame 16 → 11), with its total duration reduced as well (FAF 55 → 50).
    • Buff The arms' hitboxes have been extended towards Greninja (Z-stretch: 0 → 7), and the move has one additional hitbox at each side during the last active frame, removing its blindspots.

Aerial attacks

  • Buff All aerials have less landing lag (12 frames → 7 (neutral), 15 → 11 (forward), 13 → 10 (back), 15 → 14 (up), 32 → 30 (down)).
  • Neutral aerial:
    • Buff The move has considerably less ending lag (FAF 65 → 53), making it much less likely to cause a self-destruct offstage.
    • Buff The late hit has a longer duration (frames 14-16 → 14-19).
  • Forward aerial:
    • Buff It has much more knockback scaling (84 → 95), allowing it to KO roughly 20% earlier.
    • Buff The move has a new, smaller extended hitbox directly in front of Greninja (size: 3u; Y/Z-offset: 7.5/8; Y-stretch: 8.5), removing its blindspot.
    • Nerf The move's two other hitboxes are smaller (5.4u/4.4u → 4.7u/3.7u), and one of them is offset further from Greninja (Y-offset: -7 → -8), creating a new blindspot between them.
  • Back aerial:
    • Buff The move has less ending lag (FAF 46 → 41).
    • Buff It has bigger hitboxes (hits 1 and 2: 5u/4u/2u → 5.5u/4.3u/2.5u; hit 3: 5.8u/4.5u/2u → 5.8u/4.5u/2.5u).
    • Buff The last two hits have less startup (hit 2: frame 8 → 7; hit 3: frame 13 → 11).
    • Buff The first hit sends at different angles, one of them being a different autolink angle (365°/30°/30° → 367°/35°/35°). This allows it to connect better into the second hit.
    • Buff The third hit deals more damage (4% → 6%), with its knockback scaling not fully compensated (120 → 95), allowing it to KO slightly earlier.
  • Up aerial:
    • Buff The fifth hit uses the autolink angle like the previous hits (85° → 367°), allowing it to connect more reliably into the final hit, and increasing the move's window for drag-down setups.
    • Buff The first five hits have more base knockback (45 → 55), and the fifth hit no longer uses set knockback. This is overall beneficial to the move, as it inflicts more hitstun to opponents that further facilitates drag-down setups, without drastically disrupting its linking ability due to using the autolink angle.
  • Down aerial:
    • Buff The move has less ending lag if it misses (FAF 57 → 52), making it slightly safer to use offstage.
    • Buff Greninja no longer loses its double jump when hitting with the move.
    • Nerf It has more ending lag when it hits an opponent (FAF 13 → 21), hindering its combo potential and making it less safe on shield.
    • Nerf Its hitboxes are smaller (clean: 6u → 4.3u; late: 7u → 5.2u) and higher up (Y-offset: -2 → 0.1), reducing its range.

Throws and other attacks

  • Grab:
    • Nerf All grabs have more ending lag (standing: FAF 30 → 39; dash: 40 → 47; pivot: 36 → 42).
    • Buff Standing and pivot grab have one frame faster startup (standing: frame 11 → 10; pivot: frame 15 → 14).
    • Nerf Dash grab has slower startup (frame 9 → 13).
    • Nerf Dash grab's grabbox doesn't extend out as far (Z-stretch: 20 → 17.5), reducing its range.
    • Buff Pivot grab's grabbox extends further (Z-stretch: -22 → -25.3), increasing its range. It is now the largest non-tether pivot grab in the game.
  • Pummel:
    • Buff Pummel deals more hitlag (4 frames → 11), but has less startup (frame 6 → 2) and significantly ending lag (FAF 27 → 8). It is now one of the fastest pummels in the game, rather than one of the slowest.
    • Nerf It deals less damage (2% → 1%).
  • Change The speed of Greninja's forward, back, and up throws is no longer weight-dependent. This improves up throw's combo potential against heavyweights, but worsens it against lightweights.
  • Forward throw:
    • Buff The move has gained a hitbox before the throw, increasing its damage (5% → 3.5% (hit 1), 4.5% (throw); 8% total) and allowing it to hit bystanders.
    • Buff It launches at a lower angle (50° → 40°) with much more knockback overall (70 base/45 scaling → 65/100), to the point it has above-average knockback for a forward throw rather than being one of the weakest in the game, greatly improving its utility for setting up edgeguards and KOing at very high percents.
  • Back throw:
    • Buff Back throw deals more damage (8% → 9%).
    • Change It has an altered animation: Greninja turns towards the screen instead of remaining facing forward, and swings its arms horizontally towards its back to toss the opponent.
  • Up throw:
    • Buff Up throw has one frame less ending lag (FAF 44 → 43).
  • Down throw:
    • Buff Down throw has less ending lag (FAF 43 → 38), improving its combo potential.
  • Edge attack:
    • Buff Edge attack deals more damage (7% → 9%).
  • Down taunt:
    • Nerf Down taunt has much more ending lag (FAF 80 → 110), further reducing its very limited utility.
    • Nerf Greninja now suffers hitlag when down taunt connects, but the opponent only suffers hitlag on the ground, as the air only hitboxes are flinchless, and thus cannot inflict hitlag. This effectively reduces the move's hit rate.

Special moves

  • Water Shuriken:
    • Buff Water Shuriken has slightly increased range.
    • Buff Opponents don't fall out of the fully charged shuriken as much as before.
    • Nerf Uncharged Water Shuriken has less knockback scaling (85 → 45).
    • Change Water Shuriken looks sharper.
  • Shadow Sneak:
    • Buff It can now be used multiple times in midair.
    • Buff Shadow Sneak's shadow travels faster.
    • Buff Both attack variants have less startup.
    • Buff Forward Shadow Sneak has a new animation: it is a forward kick instead of a handstand kick. It launches at a much lower angle (48° → 36°), improving its KO potential.
    • Change Greninja now cloaks itself in a whirlwind before disappearing.
    • Nerf Shadow Sneak stalls less in the air (initial vertical boost: 2.1 → 1.8), hindering its recovery usage.
    • Nerf The shadow is notably darker, and the shadow's eyes flash red just before release. This makes it easier to predict the attack.
  • Hydro Pump:
    • Change Hydro Pump now has an arrow pointing in the direction of travel, similar to Pikachu's Quick Attack and Pichu's Agility.
    • Buff Hydro Pump can now be ledge-cancelled.
    • Buff Greninja no longer loses its double jump if it is hit out of Hydro Pump.
    • Nerf The water shots have considerably reduced knockback (65 (base)/100(scaling) → 60/80), and smaller hitboxes (6u → 4.7u), greatly reducing the move's offensive utility.
  • Substitute:
    • Buff The counter window is longer (frames 8-29 → 8-34).
    • Nerf It has more ending lag if it misses (FAF 65 → 70).
    • Buff Substitute slows down the opponent when the attack activates, allowing the attack to land more consistently.
    • Buff All of the attack's variants have one frame faster startup (frame 41 → 40).
    • Buff All of the attack's variants now grant Greninja intangibility during the attack (frames 1-37 → 1-56).
    • Nerf All of the attack's variants have slightly more ending lag (FAF 85 → 87).
    • Nerf The side variant has much less knockback scaling (100 → 85).
    • Nerf The up and diagonal up variants deal less damage (up: 14% → 13%; diagonal up: 13% → 12%) and have less knockback scaling (both: 100 → 95), noticeably hindering their KO power.
    • Nerf The down variant deals less damage (14% → 13%) and has less knockback (grounded: 100 scaling → 95; aerial: 50 base/100 scaling → 25/65). This hinders its KO power; particularly, the aerial version is no longer among the strongest meteor smashes in the game.
    • Nerf The diagonal down variant deals less damage (13% → 12%) without compensation on knockback, hindering its KO power.
    • Change Substitute has more vibrant particle effects.
  • Secret Ninja Attack:
    • Change Greninja now turns into Ash-Greninja during its Final Smash.
    • Change Greninja and its opponents are no longer silhouetted during the attack.
    • Nerf The final hit has considerably less knockback scaling (160 → 125), reducing the move's KO potential to the point where it is now weaker than the similar final smashes of Robin and Mii Brawler, both of which also deal less knockback now.

Update history

Greninja has received a mix of minor buffs and nerfs via game updates. Several glitches have also been fixed over time.

Super Smash Bros. Ultimate 1.2.0

  • Bug fix A visual glitch with Greninja's screen KO has been fixed.

Super Smash Bros. Ultimate 2.0.0

  • Buff Down smash has a larger internal hitbox (Z offset: 0u → 0u-7u).
  • Nerf Hydro Pump no longer instantly cancels Greninja's endlag when landing on a moving or slanted platform.

Super Smash Bros. Ultimate 3.0.0

  • Nerf Water Shuriken deals less shield damage (0 → (-1.5 to -5.5)/-4.5 (uncharged/fully charged, hit 6)).

Super Smash Bros. Ultimate 3.1.0

  • Bug fix Fixed an unknown glitch that resulted in Greninja sliding while shielding.

Super Smash Bros. Ultimate 4.0.0

  • Change Greninja nows immediately descends when using down aerial after being launched, rather than air stalling.

Super Smash Bros. Ultimate 7.0.0

  • Buff Overall shield size has been increased by 1.206×.

Super Smash Bros. Ultimate 8.0.0

  • Buff Pummel has a larger hitbox (5u → 6u), allowing it to connect more consistently.

Moveset

For a gallery of Greninja's hitboxes, see here.

Note: All numbers are listed as base damage, without the 1v1 multiplier.

  Name Damage Description
Neutral attack   2% Two alternating palm thrusts followed by a double palm thrust that emits a small blast of water. If button mashed, it is instead followed by a series of knifehand strikes that emit blade-shaped water blasts that concludes with an outward knifehand strike that emits a wide blast of water. It can also be jab canceled, such as into forward tilt, down tilt and forward smash.
2%
3%
0.5% (loop), 2% (last)
Forward tilt   7.3% A hook kick which stops half way. It can be angled and can lock opponents.
Up tilt   4.5% Swings its tongue upwards. A good aerial combo starter and juggling tool due to its low knockback and somewhat disjointed hitbox. It can combo into itself at low percents and is a reliable way to connect into up aerial.
Down tilt   4% Does a downward hand sweep. It sends opponents at an upward angle, making it a versatile combo starter. Notably, it can confirm a KO into an up smash rather easily.
Dash attack   8% Does a sweep kick. Is arguably one of the best dash attacks in the game, as it launches opponents at an excellent angle for combos, making it one of Greninja's best combo starters. Reliably combos into back aerial at virtually any percent, and can set up up aerial strings or drag-down combos with up aerial.
Forward smash   14% An inward slash with a water kunai. Deals good knockback and has good range. However, it has notable ending lag.
Up smash   5% (hit 1), 14% (hit 2 clean center), 11% (hit 2 clean sides), 10% (hit 2 late) Two reverse gripped inward slashes with water kunai, similar to Sheik's up smash. Greninja's strongest finisher, especially when hit clean. Can be combo'd into from a down-tilt at specific percentages for a KO.
Down smash   13% (kunai), 11% (arms) Hits both sides with water kunai. Due to it sending opponents at an semi-spike angle and coming out on frame 11, it is a quick and effective way to set up an edge-guard situation.
Neutral aerial   11% (clean), 6% (late) Strikes a ninjutsu pose while emitting an exploding water bubble. Despite noticeable start-up lag for a neutral aerial(frame 12), it boasts great combo potential at low to mid percentages with its strong and weak hits and can KO confirm into up-smash at high percents with the weak hit. It can also KO at very high percents with its strong hit.
Forward aerial   14% Slashes with a water kunai. It has some start-up and suffers from high end lag, but it is a great tool in the neutral for spacing due to its disjointed hitbox and can be used for KOing. It is also safe on shield if spaced correctly.
Back aerial   3% (hit 1), 2.5% (hit 2), 6% (hit 3) Kicks backwards three times. It is Greninja's fastest aerial attack, although it is also one of the weakest aerials of its kind. However, this makes it a useful combo tool in return, as it can be followed up from a down throw, down tilt, as well as a dash attack. It can be a situational out-of-shield option if the opponent crosses-up on its shield.
Up aerial   1.3% (hits 1-5), 3% (hit 6) Does a upward corkscrew kick, similar to both Sheik's and Joker's up aerials. One of Greninja's best combo and KO tools, as it can juggle and KO effectively due to its great jumping prowess. It also allows for drag-down combos because it's multi-hit properties, although this requires precise timing to land it at the right time, as its final launching hit comes out too fast to set up drag-down combos otherwise.
Down aerial   8% A diving double foot stomp. It acts as a stall-then-fall and bounces off opponents. The clean hit meteor smashes opponents while the late hit sends the opponent upwards, allowing for some situational combos.
Grab   — Grabs with a whirlpool. While its standing grab is slow, it is among the longest-reaching grabs in the game.
Pummel   1% Compresses target with water. Decent speed.
Forward throw   3.5% (hit 1), 4.5% (throw) Shoves the opponent forward. Can KO at high percentages near the edge.
Back throw   9% Greninja leans forward and flings the opponent backwards. Like forward throw, its decent knockback gives it good edgeguarding potential at high percentages.
Up throw   5% Tosses the opponent upwards. One of Greninja's most useful throws, as it can combo into a up tilt or up aerial at low and medium percents and can even KO at later percents.
Down throw   5% Slams the opponent onto the ground. It can combo into a down tilt, forward tilt, and dash attack at low percentages. It can combo into back aerial at medium percents and later into forward aerial as well at higher percentages with good timing.
Forward roll
Back roll
Spot dodge
Air dodge 		— —
Techs — —
Floor attack (front)
Floor getups (front) 		  8% Sweep kicks around itself while getting up.
Floor attack (back)
Floor getups (back) 		  8% Sweep kicks around itself while getting up.
Floor attack (trip)
Floor getups (trip) 		  8% Sweep kicks around itself while getting up.
Edge attack
Edge getups 		  9% Performs a roundhouse kick while climbing up.
Neutral special Water Shuriken 3%-10.8% (uncharged), 1.0% (fully charged looping hits), 9% (fully charged final hit) Uses Water Shuriken, which can be charged. Depending on how long the move is charged, the shuriken will be larger and do more damage, however the speed and distance will decrease as a result. At full charge, it hits multiple times and can kill with a Shadow Sneak follow-up at low and medium percents. It is also a decent KOing option at higher percents. A fully charged water shuriken that is reflected at a higher speed will have trouble landing the final hit on Greninja because of the looping hits not moving Greninja far enough for it.
Side special Shadow Sneak 10% (normal), 12% (reverse) Disappears briefly, then preforms a forward kick or a drop kick (relative to the user's reappearance in relation to the enemy) to attack. The move activates when the special button is released. The way the shadow moves is relative to Greninja's position, and it can be moved further or closer to change how far Greninja teleports. While performing Shadow Sneak, Greninja cannot run, attack, grab, dodge or shield. However, it can walk slowly, jump and taunt. Has strong knockback and base knockback, which allows it to kill notably early when hitting the move offstage.
Up special Hydro Pump 2% (per shot) Uses Hydro Pump to propel itself in the inputted direction; it can be used twice. Each shot has a windbox effect that pushes opponents, making it a decent option for gimping predictable recoveries.
Down special Substitute 14% (up or down), 11% (left or right) Does a pose, and if anyone hits it while posing, Greninja will temporarily disappear, get replaced by a wooden log or a Substitute doll, and then appear behind the opponent and strike them. It deviates noticeably from other counters, as the attack itself can be angled in an inputted direction and launching the opponent in that direction (with the down input meteor smashing opponents, which makes it a good punish against reckless edgeguarders).
Final Smash Secret Ninja Attack 6% (the mat), 50% (Total in the attack after mat) Turns into Ash-Greninja and attacks the opponent with a mat. If an opponent is caught in the mat, Greninja will send them up into the air and strike the opponent repeatedly in midair with its kunai, before slamming them down with a final hit.
Down taunt 0.5% While standing on one foot, Greninja holds out its hands, faces the screen, and summons small sprays of water. The sprays produce some knockback, though they're able to KO only at above 420%. A video showing the exact KO percentages at which each character can be KO'd can be found here. Unlike the rest of Greninja's taunts, this one cannot be cancelled (unless Shadow Sneak is being charged before using it).

On-screen appearance

  • Emerges from a Poké Ball, then performs a ninjutsu hand sign that emits a small burst of water from its hands.
  • Greninja's on-screen appearance

    Greninja's on-screen appearance

Taunts

  • Up Taunt: Stands upright, clasping its hands together before assuming a ninjutsu stance. The stance resembles one of its attack animations from the Pokémon series.
  • Side Taunt: Shakes head from side to side, causing its tongue to whip out in the same directions. Particles of saliva fly off with each whip.
  • Down Taunt: Poses with arms out and palms upward, and summons small sprays of water from them, which deal a small amount of damage.
  • Greninja's up taunt.

    Greninja's up taunt.

  • Greninja's side taunt.

    Greninja's side taunt.

  • Greninja's down taunt.

    Greninja's down taunt.

Idle Poses

  • Crosses arms over its body, then separates them with a flourish.
  • Hunches over and assumes a ninjutsu stance.
  • Greninja's first idle pose

    Greninja's first idle pose

  • Greninja's second idle pose

    Greninja's second idle pose

Crowd cheer

Cheer (English) Cheer (Japanese/Chinese) Cheer (Italian) Cheer (Dutch) Cheer (French)
Cheer
Custom combination of the flags of Canada, the USA, and Mexico.

Source, tweaked to fix rendering issues
Description Gre - ninja! Ge - kkou -ga! Gre - nin - ja! Gre - ninja! Am - phi - no - bi!
Cheer (German) Cheer (Spanish) Cheer (Russian) Cheer (Korean)
Cheer
Custom combination of the flags of Canada, the USA, and Mexico.

Source, tweaked to fix rendering issues
Description Quaaaaa - jutsu! Greninja! Greninja! Ya ya ya! Gre - ninja! Gae - gul - nin - ja!

Victory poses

  • Left: Does a few hand seals with splashing water, and then a ninja pose. It resembles one of its attack animations in Pokémon X and Y.
  • Up: Performs Double Team to briefly create three afterimages of itself.
  • Right: Does a flip, lands in a spinning pose, and crosses its arms.
A small excerpt of the title theme of Pokémon Red, Blue, Yellow, and Green Versions, a track which would go on to become the Pokémon main theme and the title theme for the entire series.
  • GreninjaVictoryPose1SSBU.gif
  • GreninjaVictoryPose2SSBU.gif
  • GreninjaVictoryPose3SSBU.gif

In competitive play

In the early metagame, players quickly noticed that Greninja had been buffed from Smash 4, with improved versatility and speed and, despite losing its footstool combos, gained a stronger combo game thanks to improved frame data on moves such as dash attack, up throw, down throw, and neutral air. Despite this, Greninja is not a very popular pick due to its high learning curve. Nevertheless, smashers such as Stroder, Venia, Jw, and Lea have proven that the character is a very viable pick, and Greninja has been solidified as a upper high-tier character.

Most historically significant players

Any number following the Smasher name indicates placement on the Fall 2019 PGRU, which recognizes the official top 50 players in the world in Super Smash Bros. Ultimate from July 13th, 2019 to December 15th, 2019.

See also: Category:Greninja professionals (SSBU)

Classic Mode: Your Turn, Greninja!

Greninja's congratulations screen.

Greninja fights against characters that represent different types from the Pokémon games: for example, Charizard and Bowser represent the Fire type, while Mewtwo, Ness and Lucas represent the Psychic type.

Round Opponent Stage Music Notes
1 CharizardHeadSSBU.png Charizard and BowserHeadSSBU.png Bowser Pokémon Stadium Battle! (Elite Four) / Battle! (Solgaleo/Lunala) Represents Fire-type. Charizard's Pokémon Trainer is absent.
2 PikachuHeadSSBU.png Pikachu, PichuHeadSSBU.png Pichu, and ZeroSuitSamusHeadSSBU.png Zero Suit Samus Pokémon Stadium 2 Battle! (Steven) Represents Electric-type.
3 LucarioHeadSSBU.png Lucario, RyuHeadSSBU.png Ryu, and KenHeadSSBU.png Ken Pokémon Stadium Battle! (Reshiram / Zekrom) Represents Fighting-type.
4 IvysaurHeadSSBU.png Ivysaur Pokémon Stadium Battle! (Gladion) Represents Grass-type. Ivysaur's Pokémon Trainer is absent.
5 MewtwoHeadSSBU.png Mewtwo, NessHeadSSBU.png Ness, and LucasHeadSSBU.png Lucas Pokémon Stadium 2 Battle! (Dialga/Palkia) / Spear Pillar Represents Psychic-type.
6 SquirtleHeadSSBU.png Squirtle and GreninjaHeadBlackSSBU.png Greninja Kalos Pokémon League Battle! (Champion) - Pokémon X / Pokémon Y Represents Water-type. Squirtle's Pokémon Trainer is absent. The CPU will be the GreninjaHeadSSBU.png default Greninja if the player chooses the black costume.
Bonus Stage
Final Master Hand Final Destination Master Hand (Less than 7.0 intensity)
Master Hand / Crazy Hand (Intensity 7.0 or higher)		 On intensity 7.0 and higher, Crazy Hand fights alongside Master Hand.

Note: All rounds except the sixth round take place on Pokémon Stadium and Pokémon Stadium 2. If applicable, each stage will also shift to their appropriately-typed form at the earliest possible opportunity. (The stages remain in their default form in rounds 3 and 5, as none of the stages have Psychic or Fighting-themed forms.)

Credits roll after completing Classic Mode. Completing it as Greninja has Battle! (Trainer Battle) - Pokémon X / Pokémon Y accompany the credits.

Role in World of Light

Finding Greninja in World of Light

Greninja was among the fighters that were summoned to fight the army of Master Hands.

During the opening cutscene, Greninja was present on the cliffside when Galeem unleashed his beams of light. Greninja leaped into the air to avoid one of the beams, which hit Lucario instead. Greninja was hit shortly after and vaporized, getting imprisoned by Galeem afterward along with the other fighters, sans Kirby. A puppet fighter cloned from Greninja is later seen alongside ones cloned from Fox, Samus, Link and other fighters.

Greninja was one of the many fighters that fell under Dharkon's control upon Galeem's first defeat, and it can be found in the Mysterious Dimension at The Dark Realm. It can be seen impeding the path, making it an obligatory unlock.

Greninja is later seen among several other fighters, making their last stand against Galeem and Dharkon. It also shows up in the bad ending where Galeem emerges victorious against Dharkon, witnessing Galeem engulf the world in light.

Fighter Battle

No. Image Name Type Power Stage Music
50
Greninja SSBU.png
 Greninja
Shield
Shield
 10,600 Kalos Pokémon League (Ω form) Battle! (Trainer Battle) - Pokémon X / Pokémon Y

Spirit

Greninja's fighter spirit can be obtained by completing Classic Mode. It is also available periodically for purchase in the shop for 300 Gold, but only after Greninja has been unlocked. Unlocking Greninja in World of Light allows the player to preview the spirit below in the Spirit List under the name "???". As a fighter spirit, it cannot be used in Spirit Battles and is purely aesthetic. Its fighter spirit has an alternate version that replaces it with its artwork in Ultimate.

  • 418. Greninja

    418. Greninja

In Spirit battles

As the main opponent

Spirit Battle parameters Inspiration
No. Image Name Series Enemy Fighter(s) Type Power Stage Rules Conditions Music Character
154
SSBU spirit Winky.png
 Winky Donkey Kong Series •Greninja GreninjaHeadGreenSSBU.png
Attack
 1,700 Mushroom Kingdom U N/A •The enemy deals damage when falling
•The enemy has increased jump power 		Jungle Level (Brawl)
199
SSBU spirit Zora.png
 Zora The Legend of Zelda Series •Greninja GreninjaHeadVioletSSBU.png
Shield
 1,800 Great Bay N/A •The enemy's neutral special has increased power Ocarina of Time Medley
385
SSBU spirit Slippy Toad.png
 Slippy Toad Star Fox Series •Greninja GreninjaHeadGreenSSBU.png
•Fox FoxHeadBlackSSBU.png
Shield
 9,600 Frigate Orpheon (hazards off) N/A •Defeat the main fighter to win
•Timed battle (1:30)
•The enemy tends to avoid conflict 		Corneria - Star Fox
482
SSBU spirit Raikou, Entei, & Suicune.png
 Raikou, Entei, & Suicune Pokémon Series •Greninja GreninjaHeadVioletSSBU.png
•Incineroar IncineroarHeadWhiteSSBU.png
•Pikachu PikachuHeadLibreSSBU.png
Shield
 9,900 Suzaku Castle •Hazard: Lava Floor •The floor is lava Pokémon Red / Pokémon Blue Medley Suicune
516
SSBU spirit Darkrai.png
 Darkrai Pokémon Series •Greninja GreninjaHeadBlackSSBU.png
Shield
 9,900 Luigi's Mansion (Ω form) •Item: Black Hole
•Hazard: Slumber Floor 		•The floor is sleep-inducing
•Only certain Pokémon will emerge from Poké Balls (Darkrai) 		Battle! (Team Galactic)
770
from the game files
 Metal Gear RAY Metal Gear Solid Series •Metal Greninja GreninjaHeadGreySSBU.png (140 HP)
Grab
 4,200 Shadow Moses Island •Item: Exploding Types •Stamina battle
•Explosion attacks aren't as effective against the enemy
•The enemy is metal 		Yell "Dead Cell"
893
SSBU spirit Shadow Man.png
 Shadow Man Mega Man Series •Greninja GreninjaHeadPurpleSSBU.png×3 (60 HP)
Shield
 3,500 Norfair (Battlefield form) N/A •The enemy's neutral special has increased power
•Stamina battle
•The enemy favors neutral specials 		Shadow Man Stage
1,014
SSBU spirit Luka.png
 Luka Bayonetta Series •Greninja GreninjaHeadBlackSSBU.png
Shield
 3,800 New Donk City Hall •Temporary Invincibility •The enemy becomes temporarily invincible when badly damaged Riders Of The Light
1,048
from the game's files
 Octoling Octopus Splatoon Series •Greninja Team GreninjaHeadPinkSSBU.png×4
Shield
 3,900 Moray Towers N/A •Timed battle (2:00) Octoweaponry
1,143
Sable Prince
 Frog & Snake Kaeru no Tame ni Kane wa Naru •Greninja GreninjaHeadGreenSSBU.png
•King K. Rool KingKRoolHeadBlueSSBU.png
Shield
 3,600 Dream Land GB (Castle Lololo interior) •Assist Trophy Enemies (Sablé Prince) •Hostile assist trophies will appear Kirby Retro Medley (Castle Lololo) Frog
1,291
Ninjara
 Ninjara ARMS •Greninja GreninjaHeadGreenSSBU.png
Grab
 3,600 Suzaku Castle •Item: Boomerang •The enemy has increased move speed Ninja College
•Mii Brawler MiiBrawlerHeadSSBU.png (Moveset 2313, Ninjara Wig, Ninjara Outfit)[SB 1]
  1. ^ This alternative occurs when the corresponding DLC has been purchased and downloaded.

Alternate costumes

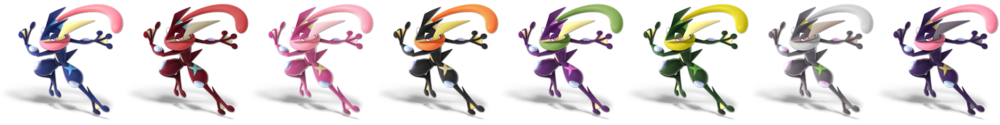
Greninja Palette (SSBU).png
GreninjaHeadSSBU.png GreninjaHeadRedSSBU.png GreninjaHeadPinkSSBU.png GreninjaHeadBlackSSBU.png GreninjaHeadVioletSSBU.png GreninjaHeadGreenSSBU.png GreninjaHeadGreySSBU.png GreninjaHeadPurpleSSBU.png

Gallery

Fighter Showcase Video

Trivia

  • In the Pokémon series, Ash-Greninja is only obtainable as a male. The fact that Greninja transforms into Ash-Greninja for its Final Smash, Secret Ninja Attack, implies that Greninja is a male in Ultimate.
  • Greninja's new character portrait resembles its air dodge animation.
    • It also resembles Fox's character portrait from Super Smash Bros. 4 but with the arm and leg positions mirrored.
  • Greninja's fighter number, 50, is the same as the number of its costume in Super Mario Maker. It shares this distinction with Inkling.
  • Greninja, Ivysaur, Olimar, Little Mac, Ryu and Ken are the only characters to never appear as minions in any Spirit battles.
  • Alongside Luigi, Greninja is one of two characters in Ultimate with a taunt that cannot be cancelled, due to the fact that their non-cancelable taunts have hitboxes.
    • Strangely, this does not apply for Snake and Kazuya's taunts that have damaging hitboxes
    • Greninja and Luigi are also the only two characters whose Classic Mode titles feature their names.
  • Greninja can also be unlocked immediately after clearing Classic Mode as Sheik, referencing their ninja-like traits and movements.
  • Greninja appears slightly tilted in its damage meter compared to its character artwork. This distinction is shared with fellow Pokémon series character Incineroar.
    • Coincidentally, both are final evolutions of starter Pokémon and both have Dark as their secondary type.
    • Both are also found and unlocked in the Dark Realm in World of Light.
  • Incineroar and Jigglypuff are the only Pokémon that are not encountered in Greninja's Classic Mode route.
  • Oddly, Greninja does not vanish when performing a directional air dodge despite the sound effects playing. It shares this oddity with Rosalina & Luma and Palutena.
  • In Ultimate, Greninja has a weight of 88, which almost matches its weight in Pokémon (in pounds), being 88.2 lbs.


v • d • e
Fighters in Super Smash Bros. Ultimate
Veterans Bayonetta · Bowser · Bowser Jr. · Captain Falcon · Cloud · Corrin · Dark Pit · Diddy Kong · Donkey Kong · Dr. Mario · Duck Hunt · Falco · Fox · Ganondorf · Greninja · Ice Climbers · Ike · Jigglypuff · King Dedede · Kirby · Link · Little Mac · Lucario · Lucas · Lucina · Luigi · Mario · Marth · Mega Man · Meta Knight · Mewtwo · Mii Fighter (Mii Brawler · Mii Gunner · Mii Swordfighter) · Mr. Game & Watch · Ness · Olimar · Pac-Man · Palutena · Peach · Pichu · Pikachu · Pit · Pokémon Trainer (Charizard · Ivysaur · Squirtle) · R.O.B. · Robin · Rosalina & Luma · Roy · Ryu · Samus · Sheik · Shulk · Snake · Sonic · Toon Link · Villager · Wario · Wii Fit Trainer · Wolf · Yoshi · Young Link · Zelda · Zero Suit Samus
Newcomers Banjo & Kazooie · Byleth · Chrom · Daisy · Dark Samus · Hero · Incineroar · Inkling · Isabelle · Joker · Kazuya · Ken · King K. Rool · Min Min · Piranha Plant · Pyra / Mythra  · Richter · Ridley · Sephiroth · Simon · Sora · Steve · Terry
v • d • e
PokemonSymbol.svg Pokémon universe
Fighters Pikachu (SSB · SSBM · SSBB · SSB4 · SSBU) · Jigglypuff (SSB · SSBM · SSBB · SSB4 · SSBU) · Pichu (SSBM · SSBU) · Mewtwo (SSBM · SSB4 · SSBU) · Pokémon Trainer (SSBB · SSBU) · Squirtle (SSBB · SSBU) · Ivysaur (SSBB · SSBU) · Charizard (SSBB · SSB4 · SSBU) · Lucario (SSBB · SSB4 · SSBU) · Greninja (SSB4 · SSBU) · Incineroar (SSBU)
Boss Rayquaza
Stages Saffron City · Pokémon Stadium · Poké Floats · Pokémon Stadium 2 · Spear Pillar · Unova Pokémon League · Prism Tower · Kalos Pokémon League
Items Poké Ball · Master Ball
Poké Ball Pokémon Abomasnow · Abra · Arceus · Articuno · Beedrill · Bellossom · Bewear · Blastoise · Bonsly · Celebi · Chansey · Charizard · Chespin · Chikorita · Clefairy · Cyndaquil · Darkrai · Dedenne · Deoxys · Ditto · Eevee · Electrode · Entei · Exeggutor · Fennekin · Fletchling · Gardevoir · Genesect · Giratina · Gogoat · Goldeen · Groudon · Gulpin · Hitmonlee · Ho-Oh · Inkay · Jirachi · Keldeo · Koffing · Kyogre · Kyurem · Latias & Latios · Lugia · Lunala · Manaphy · Marill · Marshadow · Meloetta · Meowth · Metagross · Mew · Mimikyu · Moltres · Munchlax · Onix · Oshawott · Palkia · Piplup · Porygon2 · Pyukumuku · Raichu · Raikou · Scizor · Snivy · Snorlax · Solgaleo · Spewpa · Starmie · Staryu · Suicune · Swirlix · Tapu Koko · Togedemaru · Togepi · Torchic · Unown · Venusaur · Victini · Vulpix · Weavile · Weezing · Wobbuffet · Xerneas · Zapdos · Zoroark
Enemies Chandelure · Cryogonal · Gastly · Koffing · Petilil
Other Charmander · Cresselia · Dialga · Porygon · Registeel · Reshiram · Team Rocket · Zekrom · List of Pokémon
Trophies, Stickers and Spirits Trophies (SSBM · SSBB · SSB4) · Stickers · Spirits
Music Brawl · SSB4 · Ultimate
Retrieved from "https://www.ssbwiki.com/index.php?title=Greninja_(SSBU)&oldid=1660958"