Winged Form

The Winged Form is Sephiroth's fighter ability in Super Smash Bros. Ultimate. It activates when he has taken a certain amount of damage, causing him to unfurl a singular black wing from his right shoulder (which takes on a purple glow) and announce 身の程を知れ ("Know your place") or 目障りだ ("Pathetic"), while the screen briefly acquires a dark tint. Once Sephiroth's Winged Form is active, he gains a variety of benefits, including a third jump, increased damage output, faster movement speed, and damage-based armor on all his smash attacks that resists up to 20%. Sephiroth loses the form after being KO'd, or through a system of points that gradually decrease as he deals damage or KOs opponents. Once Sephiroth loses his Winged Form, he cannot regain it back until he gets KO'd.
Technical information[edit]
Activation[edit]
As stated by Masahiro Sakurai, Winged Form activates when Sephiroth is "in danger". More specifically, Sephiroth's danger status is determined not only by his damage percentage after getting hit, but also his current placing in the match; if he has a stock or score advantage, his Winged Form will activate at later percents, whereas if he has a stock or score disadvantage, it will activate at earlier percents. Stock/score advantage and disadvantage are both capped at two for the ability's activation, leading to five possible cases: Sephiroth having two stocks/points less than the opponent, one less, an equal amount, one more, or two more.
In addition to these two factors, Winged Form's activation percent can be varied further by the difference between Sephiroth and the opponent's percents prior to getting hit. Generally, it activates earlier if Sephiroth's percent is higher than the opponent's, and later if the opposite is true, though the specific ranges are noticeably different for each of the five stock/score difference cases. As a result, the specific activation percent follows a highly intricate algorithm, and is difficult to determine precisely during matches.
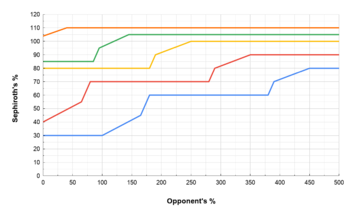
The following table summarizes all the percent ranges at which Winged Form can activate in a 1v1 battle, based on Sephiroth's stock/score and percent differences with the opponent (the latter which is marked as diff, with a positive value meaning Sephiroth's percent is higher).
| Stock/score difference | Percent difference | Activation percent | Formula |
|---|---|---|---|
| -2 | > -70 | 30% | N/A |
| ≤ -70, ≥ -120 | 30%-45% | 45 - 0.3 * (120 + diff)
| |
| < -120, > -320 | 60% | N/A | |
| ≤ 320, ≥ -370 | 70%-80% | 70 - 0.2 * (320 - diff)
| |
| < -370 | 80% | N/A | |
| -1 | > 40 | 40% | N/A |
| ≤ 40, ≥ -10 | 40%-55% | 55 - 0.3 * (10 + diff)
| |
| < -10, > -210 | 70% | N/A | |
| ≤ -210, ≥ -310 | 80%-90% | 80 - 0.2 * (210 - diff)
| |
| < -310 | 90% | N/A | |
| 0 | > -100 | 80% | N/A |
| ≤ -100, ≥ -150 | 90%-100% | 90 - 0.2 * (100 - diff)
| |
| < -150 | 100% | N/A | |
| +1 | > 10 | 85% | N/A |
| ≤ 10, ≥ -40 | 95%-105% | 95 + 0.2 * (10 - diff)
| |
| < -40 | 105% | N/A | |
| +2 | > 120 | 90% | N/A |
| ≤ 120, ≥ 70 | 100%-110% | 100 + 0.2 * (120 - diff)
| |
| < 70 | 110% | N/A |
The following table shows examples of how the activation percents for each stock/score difference change with the opponent's percent (assuming it remains static for each case). Overall, the ability favors Sephiroth being at a disadvantage, with more drastic changes in percent compared to being at an advantage.
| Opponent's percent | Activation percent | ||||
|---|---|---|---|---|---|
| -2 | -1 | 0 | +1 | +2 | |
| 0% | 30% | 40% | 80% | 85% | 103.34% |
| 50% | 30% | 51.54% | 80% | 85% | 110% |
| 100% | 30% | 70% | 80% | 97.5% | 110% |
| 150% | 41.54% | 70% | 80% | 105% | 110% |
| 200% | 60% | 70% | 91.67% | 105% | 110% |
Deactivation[edit]
For deactivation, Winged Form follows a system of points. Upon activation, a set amount of points is granted to Sephiroth depending on his stock/score difference with the opponent, once again with five possible cases. From two stocks behind to two stocks ahead, this corresponds to 110, 100, 90, 65, and 50 points, respectively. Afterwards, these points can be lost, and Winged Form deactivates once Sephiroth has no points remaining (or if he gets KO'd, which removes all points alongside Winged Form).
Points are lost via the following conditions:
- Attacking opponents reduces points by an amount equal to 0.3× of the damage dealt, or 0.15× in battles with multiple opponents. This ignores all damage modifiers, including stale-move negation, the 1v1 multiplier, or Winged Form's own multiplier.
- For each respective stock/score difference case, all points are lost if Sephiroth deals up to 366.7%, 333.4%, 300%, 216.7%, and 166.7% base damage.
- KOing an opponent removes 50 points. In addition to this, the amount of points after a KO is changed dynamically based on the new stock/score difference. For example, if Sephiroth was given 90 points (equal stocks) and KOs the opponent without dealing any damage, they are reduced to 40, then again to 15 with the updated stock/score difference (one stock ahead, which would grant 65 points), so dealing at least 50% base damage will deactivate Winged Form. Likewise, if he was given 100 points (one stock behind), they are reduced to 50 by the KO, then to 40 by the new stock/score difference, causing Winged Form to deactivate with at least 133.4% base damage dealt. As a result, Winged Form is generally lost quickly after getting a KO, unless Sephiroth is at a disadvantage.
Differences in other modes[edit]
In Training mode, Winged Form's activation and deactivation are noticeably different than in other modes. The activation percent instead matches the opponent's current percent (whether Sephiroth is used by the player or the CPU), with a minimum of 65% and a maximum of 90%, causing it to activate at 65% if the opponent has no damage. Score differences are completely ignored for both the activation percent and points earned; instead, Sephiroth always earns 110 points, with the conditions to lose them remaining unchanged.
In Stamina mode, while the points system remains the same, Winged Form instead activates when Sephiroth has 35% or less of his starting HP left. Like in standard battles, stock/score and HP differences with the opponent affect this threshold, though their specifics are currently unknown.
Effects[edit]
Stat increases[edit]
In addition to the listed stat increases, Winged Form grants Sephiroth an additional midair jump (giving him a total of three jumps), and a 1.3× damage multiplier to all his attacks, with the exception of items and Supernova. For the damage multiplier, only the difference in the opponent's resulting percent is taken into account for the knockback formula, so how early an attack can KO is equal to its damage difference with the multiplier (for example, if an attack deals 10% normally, it will KO 3% earlier with Winged Form active).
| Stat | Base value | Multiplier | Resulting value |
|---|---|---|---|
| Walk acceleration | 0.1 | 1.15× | 0.115 |
| Walk speed | 0.9 | 1.15× | 1.035 |
| Dash speed | 1.92 | 1.2× | 2.304 |
| Run acceleration | 0.12 | 1.2× | 0.144 |
| Run speed | 1.86 | 1.25× | 2.325 |
| Traction | 0.11 | 1.3× | 0.143 |
| Air acceleration (base) | 0.01 | 1.15× | 0.0115 |
| Air acceleration (additional) | 0.07 | 1.1× | 0.077 |
| Air speed | 0.95 | 1.2× | 1.14 |
| Air friction | 0.008 | 1.05× | 0.0084 |
| Gravity | 0.108 | 1.03× | 0.11124 |
| Fall speed | 1.84 | 1.05× | 1.932 |
Smash attack armor[edit]
Winged Form grants armor to all of Sephiroth's smash attacks, which is active from their charge point until their hitboxes come out. Worth noting is that this is damage-based armor with a threshold of 20%, and not super armor, contrary to what is stated in-game and commonly believed; as a result, it cannot withstand other highly-damaging attacks.
| Smash attack | Charge frame | Armor frames | Hitbox duration | FAF |
|---|---|---|---|---|
| Forward smash | 9 | 10-23 | 24-25 | 68 |
| Up smash | 13 | 14-22 | 23-28 | 64 |
| Down smash | 9 | 10-20 | 21-23 | 54 |
Gallery[edit]
Origin[edit]
Winged Form is an allusion to his "Safer∙Sephiroth" form and his "One-Winged Angel" theme to symbolize his Fallen Hero status. Sephiroth's black wing first appeared in Kingdom Hearts and it later made appearances in the Compilation of Final Fantasy VII, Final Fantasy VII Remake as well as the fighting game Dissidia Final Fantasy, where it appears as Reunion, his EX mode. The staff of Crisis Core stated that the reason why the wing was black was to suggest evil.[1]
Names in other languages[edit]
References[edit]
- ^ Crisis Core: Final Fantasy VII 10th Ultimania